1. Inicio
  2. Matemáticas 2
  3. Unidad 1
  4. Problemas con ecuaciones cuadráticas
  5. Caída libre
  6. Ejercicio 3

Ejercicio 3

Caída Libre

Con este ejercicio analizarás las condiciones que se establecen en el enunciado de un problema de caída libre, mediante la identificación entre lo conocido y lo desconocido, para expresar las relaciones entre los datos con una ecuación cuadrática.

Ejercicio de arrastrar

Lee el problema que se plantea y luego arrastra los datos conocidos, desconocidos y la expresión matemática de la caída libre a los recuadros de la tabla, según corresponda. Las opciones correctas se marcarán en verde y las incorrectas en rojo.

Problema

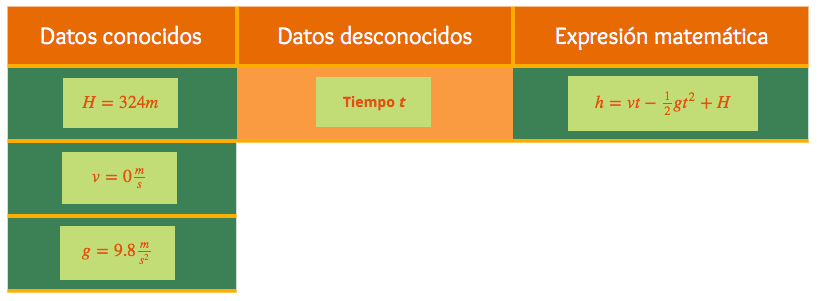
La torre Eiffel tiene una altura de 324 metros sobre la tierra, desde la parte superior se deja caer una pelota de golf. Determina el tiempo que le toma llegar al suelo.

Arrastra
  • Tiempo t
  • $h=vt- \frac {1} {2} gt^2+H$
  • $ v=0 \frac {m}{s} $
  • $ g=9.8 \frac{m}{s^2} $
  • $ H=324 m$
Datos conocidos Datos desconocidos Expresión matemática

Las opciones correctas se han marcado en color verde, las incorrectas en color rojo.

Respuestas correctas:

respuestas

Ejercicio de escritura

En tu cuaderno de notas sustituye en la expresión algebraica de caída libre los datos conocidos y determina el tiempo que requiere la pelota de golf para llegar al suelo. Escribe el resultado con dos decimales en el cuadro correspondiente. Al terminar da clic en Verificar para que revises tu respuesta.

t=8.13s

El resultado se obtiene con el siguiente procedimiento:

$h=vt- \frac {1} {2} gt^2+H$

Expresión de caída libre

$h=0-\frac {1} {2} (9.8)t^2+324$

Parte del reposo con v=0 $\frac {m} {s}$

$0=-4.9t^2+324$

La pelota llega al suelo

$ 0+4.9t^2=-4.9t^2+4.9t^2+324 $

Sumar $4.9t^2$ a los lados de la ecuación para simplificarla

$4.9t^2=324$

Simplificar los lados de la ecuación

$ \frac {4.9t^2} {4.9} = \frac {324} {4.9}$

Dividir los lados de la ecuación por 4.9 para despejar $t^2$

$t^2=66.12$

Realizar operaciones

$ t= \pm \sqrt {66.12}$

Extraer la raíz cuadrada a los lados de la ecuación

$ t=±8.13 s$

Obtener el valor de la raíz cuadrada

$ t=8.13 s$

Considerar el tiempo positivo, ya que el negativo no tiene sentido en el contexto el problema
Para que puedas verificar tu respuesta debes llenar el campo.