Factorización por tanteo y uso de la propiedad del producto nulo
Una forma de resolver ecuaciones cuadráticas completas es mediante la factorización por tanteo y haciendo uso de la propiedad del producto nulo.
A continuación te presentamos dos ejemplos en los que se indica el paso a paso para su resolución.
Antes de ver el ejemplo, recordemos que un trinomio cuadrado no perfecto es el resultado de multiplicar dos binomios del tipo:
(x+a)(x+b)
Donde el valor de a y el valor de b son diferentes.
Así pues, tenemos que:
(x+a)(x+b)=ax2+bx+c=0
Entendido esto ahora resolvamos la ecuación:
x2+2x−8=0
Ubicar los valores: a=1 b=2 c=−8
Buscar dos números que multiplicados den el valor de c y a la vez sumados den el valor de b. En este caso hay que buscar dos números cuyo producto sea −8 y que éstos mismos números sumen 2.
En este caso tenemos que los valores buscados son: 4 y −2.
(x+4)(x−2)=0
Y verificamos que en realidad se cumpla que el producto dé como resultado el polinomio x2+2x−8=0 planteado en un inicio:
Multiplicamos extremos por extremos y medios por medios:
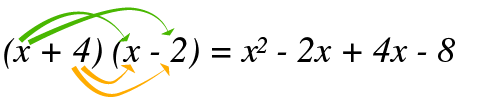
Simplificando términos en el lado derecho, comprobamos que es la misma ecuación planteada en un inicio:
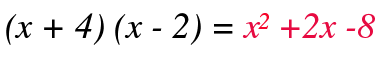
Resolvemos ambas ecuaciones aplicando la propiedad de producto nulo y encontramos la solución de la ecuación cuadrática.
Ecuación 1
x+4=0
x = 0 – 4
x = -4
Ecuación 2
x - 2 = 0
x = 0 + 2
x = 2
Estas son las dos soluciones.
Ahora para resolver la ecuación:
x^2-7x+12=0
Buscamos dos números que:
multiplicados den +12
sumados den -7
Para encontrar esos números, se descompone el término independiente (valor c) en factores de solamente números primos:
12=(3)(2)(2)(1)
Ahora comprobamos que, al formar parejas en las que se usen los factores hallados, multiplicados den 12 y sumados den -7:
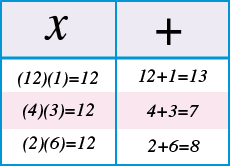
Observamos que el segundo renglón es el que cumple con la condición, sin embargo para que la suma sea -7, los factores deberán tener signo negativo:

Comprobamos el producto de binomios:
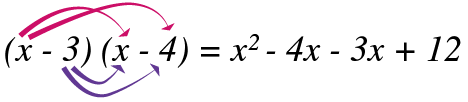
Ordenando términos:
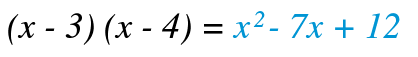
Aplicando la propiedad de producto nulo, tenemos:
Ecuación 1
x - 3 = 0
x = 0 + 3
x = 3
Ecuación 2
x - 4 = 0
x = 0 + 4
x = 4
Estas son las dos soluciones.


