Deducción de la fórmula general de segundo grado
Una ecuación de segundo grado o ecuación cuadrática de una variable es una ecuación que tiene una expresión algebraica con términos cuyo grado máximo es dos. La expresión general de una ecuación cuadrática de una variable es:
ax2+bx+c=0; para a ≠0
Y los elementos que la conforman son los siguientes:
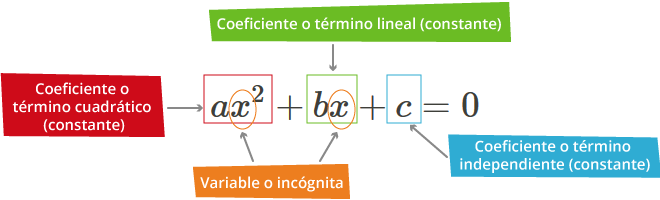
A continuación veremos cómo deducir la fórmula general por medio del trinomio cuadrado perfecto. El primer paso para deducir la fórmula general es encontrar la solución de un caso particular. El segundo paso es generalizarla, intercambiando las constantes por literales.
Para llevar a cabo el primer paso, partamos del siguiente problema:
−x2+7x−10=0
Revisa el proceso dando clic en los números
Dividir entre -1 para dejar el coeficiente o término cuadrático en 1:
x2−7x+10=0
Restar 10 en ambos lados de la ecuación para dejar el término cuadrático y lineal solos:
x2−7x+10−(10)=0−(10)
el resultado es x2−7x=−10
Para completar el trinomio cuadrado perfecto del lado izquierdo de la ecuación:
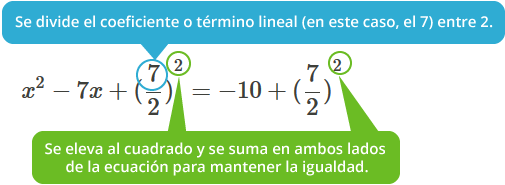
Ahora debemos factorizar el lado izquierdo de la ecuación. El resultado es el siguiente:
(x−72)2=−10+(72)2
Al simplificar el término cuadrático del lado derecho, la ecuación queda así:
(x−72)2=−10+7222
Para despejar a x, se obtiene la raíz cuadrada de ambos lados de la ecuación:
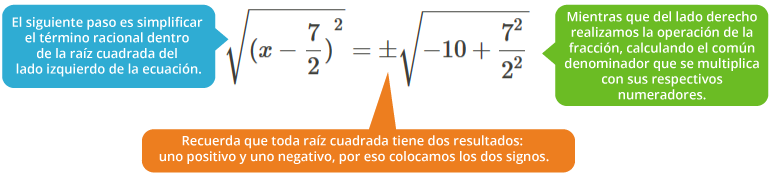
El resultado es el siguiente:
x−72=±√−10(22)+7222
Aplicando el radical en el numerador y denominador del lado derecho de la ecuación tenemos que:
x−72=±√−10(22)+72√22

Para continuar con el despeje de la variable X sumamos de ambos lados de la ecuación 7/2:
x−72+72=±√−10(22)+722+72
La expresión que queda es:

Ahora revisa el segundo paso para deducir la fórmula general. Da clic en generalización.


