Solución de la forma $(ax+b)(cx+d)=0$

Para tener mayor comprensión sobre la solución del tipo de forma $(ax+b)(cx+d)=0$ se presentan dos ejemplos específicos, obsérvalos con atención haciendo clic en las pestañas.

Solución de la ecuación $(3x+4)(2x-12)=0$

Esta ecuación particular se obtiene de la forma $(ax+b)(cx+d)=0$ con los valores $a=3$ , $b=4$ , $c=2$ y $d=-12$ como se muestra a continuación:

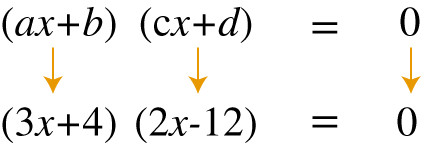
Para resolver esta ecuación se observa que el producto de los dos factores $3x+4$ y $2x-12$ es igual a cero, lo que implica que cada uno de los factores puede ser cero (propiedad del producto nulo).

Revisa el proceso dando clic en los números

$(3x+4)(2x-12)=0$

$3x+4=0$ o $2x-12=0$

Ya que el producto de $3x+4$ con $2x-12$ es 0, implica que cada uno de los factores puede ser cero.

$(3x+4)(2x-12)=0$

$3x+4=0$ o $2x-12=0$

$3x+4=0$

Resolver la ecuación $3x+4=0$ .

$(3x+4)(2x-12)=0$

$3x+4=0$ o $2x-12=0$

$3x+4=0$

$3x+4-4=0-4$

Para despejar la variable $x$ , se resta 4 a cada lado de la ecuación.

$3x=-4$

Simplifica la ecuación.

$(3x+4)(2x-12)=0$

$3x+4=0$ o $2x-12=0$

$3x+4=0$

$3x+4-4=0-4$

$3x=-4$

$\frac{3x}{3}=\frac{-4}{3}$

Para continuar con el despeje de la variable x se divide entre 3 cada lado de la ecuación.

$(3x+4)(2x-12)=0$

$3x+4=0$ o $2x-12=0$

$3x+4=0$

$3x+4-4=0-4$

$3x=-4$

$\frac{3x}{3}=\frac{-4}{3}$

$x=-\frac{4}{3}$ por tanto $x_1=-\frac{4}{3}$

Al simplificar se obtiene la solución 1.

$(3x+4)(2x-12)=0$

$3x+4=0$ o $2x-12=0$

$3x+4=0$

$3x+4-4=0-4$

$3x=-4$

$\frac{3x}{3}=\frac{-4}{3}$

$x=-\frac{4}{3}$ por tanto $x_1=-\frac{4}{3}$

De $2x-12=0$

Resolver la ecuación $2x-12=0$ .

$(3x+4)(2x-12)=0$

$3x+4=0$ o $2x-12=0$

$3x+4=0$

$3x+4-4=0-4$

$3x=-4$

$\frac{3x}{3}=\frac{-4}{3}$

$x=-\frac{4}{3}$ por tanto $x_1=-\frac{4}{3}$

De $2x-12=0$

$2x-12+12=0+12$

Sumar 12 a cada lado de la ecuación.

$2x=12$

Simplifica la ecuación.

$\frac{2x}{2}=\frac{12}{2}$

Dividir entre 2 cada lado de la ecuación.

$x=6$ , por tanto $x_2=6$

Simplificando, se obtiene la segunda solución.

Comprobación

Para realizar la comprobación se sustituye cada una de las soluciones encontradas en la ecuación original $(3x+4)(2x-12)=0$ y verifica que se cumpla la igualdad:

Para $x_1=-\frac{4}{3}$

$(3x+4)(2x-12)=0$

$[3(-\frac{4}{3})+4][2(-\frac{4}{3})-12]=0$

$[-4+4][-\frac{8}{3}-12]=0$

$[0][-\frac{44}{3}]=0$

$0=0$

Con $x_2=6$

$(3x+4)(2x-12)=0$

$[3(6)+4][2(6)-12]=0$

$[18+4][12-12]=0$

$[22][0]=0$

$0=0$

Como se cumple la igualdad, las soluciones encontradas son correctas.

Solución de la ecuación $(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

Esta ecuación presenta la misma estructura de la forma $(ax+b)(cx+d)=0$ en donde $a=\frac{3}{5}$ , $b=-2$ , $c=\frac{4}{3}$ y $d=\frac{1}{6}$ . Para resolverla, se observa que el producto de los factores $\frac{3}{5}x-2$ y $\frac{4}{3}x+\frac{1}{6}$ es igual a cero, lo que implica que cada uno de los números (factores) puede ser cero.

Revisa el proceso dando clic en los números

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

Ya que el producto de $\frac{3}{5}x-2$ con $\frac{4}{3}x+\frac{1}{6}$ es cero, implica que cada uno de los factores puede ser cero.

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

De $\frac{3}{5}x-2=0$

Resolviendo la ecuación $\frac{3}{5}x-2=0$ .

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

De $\frac{3}{5}x-2=0$

$\frac{3}{5}x-2+2=0+2$

Para despejar la variable $x$ , se suma 2 a ambos lados de la igualdad.

$\frac{3}{5}x=2$

Simplifica la ecuación.

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

De $\frac{3}{5}x-2=0$

$\frac{3}{5}x-2+2=0+2$

$\frac{3}{5}x=2$

$\frac{\frac{3}{5}x}{\frac{3}{5}}=\frac{2}{\frac{3}{5}}$

Para terminar el despeje de la variable $x$ , se divide los dos lados de la igualdad entre $\frac{3}{5}$ .

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

De $\frac{3}{5}x-2=0$

$\frac{3}{5}x-2+2=0+2$

$\frac{3}{5}x=2$

$\frac{\frac{3}{5}x}{\frac{3}{5}}=\frac{2}{\frac{3}{5}}$

$x=\frac{10}{3}$ y por tanto $x_1=\frac{10}{3}$

Al simplificar se obtiene la solución 1.

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

De $\frac{3}{5}x-2=0$

$\frac{3}{5}x-2+2=0+2$

$\frac{3}{5}x=2$

$\frac{\frac{3}{5}x}{\frac{3}{5}}=\frac{2}{\frac{3}{5}}$

$x=\frac{10}{3}$ y por tanto $x_1=\frac{10}{3}$

De $\frac{4}{3}x+\frac{1}{6}=0$

Se resuelve la ecuación $\frac{4}{3}x+\frac{1}{6}=0$

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

De $\frac{3}{5}x-2=0$

$\frac{3}{5}x-2+2=0+2$

$\frac{3}{5}x=2$

$\frac{\frac{3}{5}x}{\frac{3}{5}}=\frac{2}{\frac{3}{5}}$

$x=\frac{10}{3}$ y por tanto $x_1=\frac{10}{3}$

De $\frac{4}{3}x+\frac{1}{6}=0$

$\frac{4}{3}x+\frac{1}{6}-\frac{1}{6}=0-\frac{1}{6}$

Se resta $\frac{1}{6}$ a cada lado de la ecuación.

$\frac{4}{3}x=-\frac{1}{6}$

Simplifica la ecuación.

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$(\frac{3}{5}x-2)$ o $(\frac{4}{3}x+\frac{1}{6})=0$

De $\frac{3}{5}x-2=0$

$\frac{3}{5}x-2+2=0+2$

$\frac{3}{5}x=2$

$\frac{\frac{3}{5}x}{\frac{3}{5}}=\frac{2}{\frac{3}{5}}$

$x=\frac{10}{3}$ y por tanto $x_1=\frac{10}{3}$

De $\frac{4}{3}x+\frac{1}{6}=0$

$\frac{4}{3}x+\frac{1}{6}-\frac{1}{6}=0-\frac{1}{6}$

$\frac{4}{3}x=-\frac{1}{6}$

$\frac{\frac{4}{3}x}{\frac{4}{3}}=\frac{-\frac{1}{6}}{\frac{4}{3}}$

Para despejar la variable $x$ se divide entre $\frac{4}{3}$ cada lado de la ecuación.

$x=-\frac{3}{24}$ , y por lo tanto $x_2=-\frac{1}{8}$

Al simplificar se obtiene la solución 2.

Comprobación

Para verificar que los resultados encontrados son correctos, se sustituye cada una de las soluciones en la ecuación original $(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$ y se corrobora que se cumpla la igualdad:

Para $x_1=\frac{10}{3}$

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$[\frac{3}{5}(\frac{10}{3})-2][\frac{4}{3}(\frac{10}{3})+\frac{1}{6}]=0$

$[\frac{10}{5}-2][\frac{40}{9}+\frac{1}{6}]=0$

$[0][\frac{83}{18}]=0$

$0=0$

Para $x_2=-\frac{1}{8}$

$(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

$[\frac{3}{5}(-\frac{1}{8})-2][\frac{4}{3}(-\frac{1}{8})+\frac{1}{6}]=0$

$[-\frac{3}{40}-2][-\frac{4}{24}+\frac{1}{6}]=0$

$[-\frac{83}{40}][0]=0$

$0=0$

Como se cumple la igualdad, las soluciones encontradas son correctas.

Para saber más

Conce el procedimiento de solución para la ecuación cuadrática del tipo $(ax+b)(cx-d)=0$ .

Para realizar la división de fracciones, sigue este esquema:

$\frac{a}{b}÷\frac{c}{d}=\frac{ad}{bc}$

Alumno:

Matemáticas 2

Cuarta forma

Solución de la forma $(ax+b)(cx+d)=0$

Ejemplo 1

Solución de la ecuación $(3x+4)(2x-12)=0$

Comprobación

Ejemplo 2

Solución de la ecuación $(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$

Comprobación

Para saber más

Formulario de búsqueda

Cuarta forma

Solución de la forma (ax+b)(cx+d)=0(ax+b)(cx+d)=0

Ejemplo 1

Solución de la ecuación (3x+4)(2x−12)=0(3x+4)(2x-12)=0

Comprobación

Ejemplo 2

Solución de la ecuación (35x−2)(43x+16)=0(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0

Comprobación

Para saber más

Formulario de búsqueda

Solución de la forma $(ax+b)(cx+d)=0$

Solución de la ecuación $(3x+4)(2x-12)=0$

Solución de la ecuación $(\frac{3}{5}x-2)(\frac{4}{3}x+\frac{1}{6})=0$