Un trinomio es cuadrado perfecto si tiene la forma: $a^2+2ab+b^2$, en donde se cumple que el término central es el doble del producto de las raíces cuadradas de los términos extremos. En consecuencia, la multiplicación del binomio ${(a+b)}^2$ se puede describir como “el cuadrado del primer término; más el doble producto del primero por el segundo; más el cuadrado del tercer término”, como se muestra a continuación:

Por ejemplo, la ecuación $x^2+12x+36$ es un trinomio porque tiene tres términos (o monomios) y es cuadrado perfecto porque cumple la condición descrita en la que uno de los términos es resultado del doble producto de las raíces cuadradas de los términos restantes, es decir:

1. El primer término, $x^2$ , tiene raíz cuadrada, es decir: $x$.
2. El tercer término, $36$ , tiene raíz cuadrada, es decir: $6$.
3. El segundo término, $12x$  es resultado del doble producto de las dos raíces anteriores, es decir: $2\left(6\right)\left(x\right)$ .

Entonces, la factorización de $x^2+12x+36$ es $(x+6)(x+6)$. Esto quiere decir que los factores de $x^2+12x+36$ son $(x+6)$ y $(x+6)$, donde los términos x y 6 que los conforman son las raíces cuadradas de los términos cuadráticos $x^2$ y $36$, respectivamente.

Para factorizar un TCP es necesario identificarlo como tal, ya que existen trinomios que no son cuadrados perfectos. Por ejemplo, la expresión $x^2+x+3$ corresponde a un trinomio, pero no es cuadrado perfecto ya que no existe un binomio $(a+b)$ tal, que al elevarlo al cuadrado nos dé como resultado el trinomio. Además debe notarse que el segundo término (es decir, $x$) no se obtiene del doble producto de $x$ y $\sqrt{3}$, que son las raíces de los elementos $x^2$ y $3$. En conclusión, existen trinomios que son cuadrados perfectos y otros que no lo son.

Para saber si un trinomio de la forma $a^2+2ab+b^2$ es cuadrado perfecto, se toman los términos cuadráticos, $a^2$ y $b^2$, y se verifica que el segundo término $(2ab)$ se obtenga del doble producto de sus raíces cuadradas.

Ejemplo:

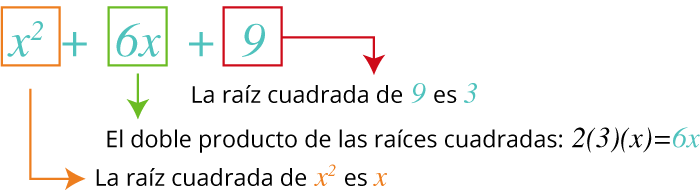
Como se comprueba que el segundo término (6x) se obtiene del doble producto de las raíces cuadradas del primer y el tercer término, entonces el trinomio dado es cuadrado perfecto.