Formalización del Trinomio Cuadrado Perfecto
En los ejemplos anteriores se presentó el procedimiento para la factorización de trinomios cuadrados perfectos, en este apartado se proporcionarán los correspondientes para la factorización de trinomios de la forma ax2+bx+c a trinomios cuadrados perfectos de la forma a(x+b)2+d.
Cuando se tiene un trinomio que no es cuadrado perfecto, entonces no se puede factorizar con los procedimientos descritos con anterioridad; en estos casos se recurre al manejo algebraico para conformar un trinomio cuadrado perfecto, con lo cual, ahora sí es posible utilizar los procedimientos ya descritos.
Revisa los siguientes ejemplos en los que se indican los pasos que se requieren para conformar un trinomio cuadrado perfecto y su posterior factorización, da clic en cada pestaña.
Dado un polinomio de la forma ax2+bx+c, para completar el TCP seguimos los siguientes pasos:
Revisa el proceso dando clic en los números
Factorizar el coeficiente del término cuadrático a, significa ponerlo como factor del paréntesis, y como el coeficiente b del término lineal x no lo tiene, se divide por el factor a, puesto que al multiplicar los términos del paréntesis por a, se obtiene ax2+bx
a(x2+bax)+c
El coeficiente de x se divide entre 2 y se eleva al cuadrado. Este resultado se ocupará en el siguiente paso.
(b2a)2
El valor del paso 2, es decir (b2a)2 se suma y resta a los elementos que están entre los paréntesis del paso 1:
a(x2+bax+(b2a)2−(b2a)2)+c
Ahora tenemos construido un trinomio cuadrado perfecto, es decir, cada término de la fracción se eleva al cuadrado:
a(x2+bax+(b2a)2−(b2a)2)+c
Donde: a(x2+bax+b24a2−b24a2)+c
TCP en naranja
Multiplicamos el factor común a al término −b24a2, para sacarlo del paréntesis:
a(x2+bax+b24a2)−ab24a2+c
Lo que queda en el paréntesis es el trinomio cuadrado perfecto
Al obtener las raíces cuadradas del primero y tercer término, el TCP se reduce a un binomio al cuadrado:
a(x2+b2a)2−ab24a2+c
Que al simplificar queda como:
a(x2+b2a)2+c−b24a
5x2+13x−6
Revisa el proceso dando clic en los números
Factorizar el coeficiente del término cuadrático a=5
5(x2+135x)−6
El coeficiente de x se divide entre 2 y se eleva al cuadrado, el producto se realiza como lo indican las líneas, es decir, el producto de extremos entre el producto de medios. Este resultado se ocupará en el siguiente paso.
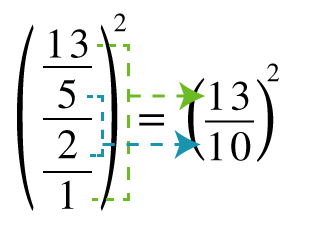
El valor del paso 2, es decir (1310)2, se suma y resta a los elementos que están entre los paréntesis del paso 1:
5(x2+135x+(1310)2−(1310)2)−6
Ahora tenemos construido un trinomio cuadrado perfecto, es decir, cada término de la fracción se eleva al cuadrado:
5(x2+135x+(13)2(10)2−(13)2(10)2)−6
TCP en naranja
Multiplicamos el factor común a al término −b24a2, para sacarlo del paréntesis.
5(x2+135x+(13)2(102))−5(13)2(10)2−6
Lo que queda en el paréntesis es el trinomio cuadrado perfecto
Al obtener las raíces cuadradas del primero y tercer término, el TCP se reduce a un binomio al cuadrado:
5(x2+1310)2−5(13)2(10)2−6
Que al simplificar queda como:
5(x2+1310)2−845100−6
Donde:
−845100−6=−845100−600100=−1445100
Por lo tanto:
5(x+1310)2−1445100
Por lo tanto, el polinomio original se puede expresar en términos de un TCP:
5x2+13x−6=5(x+1310)2−1445100
2x2+8x−10=0
El trinomio indicado no corresponde a un TCP ya que no se cumple la regla en la que el segundo término es igual al doble producto de las raíces cuadradas del primer y el tercer término. Por ello, se recurre al procedimiento descrito en la formalización, tal como se indica a continuación.
Revisa el proceso dando clic en los números
Sacamos el factor común a=2, de los términos con x:
2(x2+4x)−10=0
El coeficiente que acompaña a x, se divide entre 2 y se eleva al cuadrado. Este resultado se ocupará en el siguiente paso:
(42)2=(2)2
Sumamos y restamos el cuadrado del resultado del paso 2:
2(x2+4x+(2)2−(2)2)−10
=2(x2+4x+4−4)−0=0
Ahora tenemos un trinomio cuadrado perfecto:
2(x2+4x+4−4)−0=0
Multiplicamos por el factor común a=2 , al término -4, para sacarlo del paréntesis:
2(x2+4x+4)−2∗4−10=
2(x2+4x+4)−18=0
Lo que queda dentro del paréntesis es el trinomio cuadrado perfecto:
2(x2+4x+4)−18=0
Al obtener las raíces cuadradas del primer y el tercer término el TCP se reduce a un binomio al cuadrado:
2(x+2)2−18=0
Por lo tanto, la factorización del polinomio queda como:
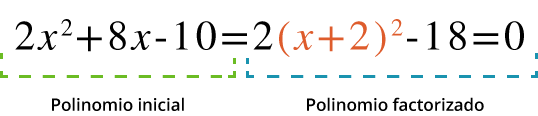
Para resolver la ecuación cuadrática 2(x+2)2−18=0, se suma 18 a los lados de la ecuación:
2(x+2)2−18+18=0+18=18
y al simplificalar se obtiene:
2(x+2)2=18
Luego se tiene que dividir a los lados de la ecuación entre 2 para eliminar el factor 2 de la misma, es decir:
2(x+2)22=182 que al simplificar queda como (x+2)2=9
Para resolverla se extrae la raíz cuadrada a los dos lados de la ecuación, es decir:
√(x+2)2=±√9 y al simplificarla se obtiene x+2=±3
Las soluciones de la ecuación cuadrática son:
x1=1
x2=−5
Comprobación
Para verificar que las soluciones encontradas son correctas, se sustituye cada solución en la ecuación original, solucionándola y corroborando que se cumpla la igualdad, como se muestra a continuación:
Para x1=1
2x2+8x−10=0
2(1)2+8(1)−10=0
2(1)+8(1)−10=0
2+8−10=0
0=0
Para x2=−5
2x2+8x−10=0
2(−5)2+8(−5)−10=0
2(25)+8(−5)−10=0
50−40−10=0
0=0
Como puede apreciarse, ambas soluciones satisfacen a la ecuación cuadrática, puesto que en cada una de ellas se obtiene 0=0 . Lo cual demuestra que x1=1 y x2=−5 son soluciones de la ecuación cuadrática 2x2+8x−10=0.


