Fórmula general
Con estas actividades podrás resolver ecuaciones de segundo grado utilizando la fórmula general.
Actividad final
Esta actividad consta de dos partes. Haz clic en cada una de ellas y lee cuidadosamente las instrucciones.
Analiza detenidamente la solución que se presenta a cada ecuación cuadrática y señala si es verdadera o falsa.
-
¿Esta solución es verdadera?
- Verdadero
- Falso
-
¿Esta solución es verdadera?
- Verdadero
- Falso
La respuesta correcta es Falso, porque la solución de la ecuación es:
$$x=\frac{-(12) \pm \sqrt{(12)^2-4(4)(9)}} {2(4)}$$
$$x_1=\frac{-12+\sqrt{0}}{8}=\frac{-12}{8}=-\frac{3}{2}$$
$$x_2=\frac{-12+\sqrt{0}}{8}=\frac{-12}{8}=-\frac{3}{2}$$
Por lo tanto, la solución de la ecuación es:
$$x_1=-\frac{3}{2}$$
$$x_2=-\frac{3}{2}$$
-
¿Esta solución es verdadera?
- Verdadero
- Falso
1. Tenemos la siguiente ecuación cuadrática: $x^2-3x+2=0$
Los coeficientes en este caso son $a=1$, $b=-3$, $c=2$
$$x=\frac{-b\pm{}\sqrt{b^2-4ac}}{2a}$$
Sustituyendo los coeficientes en la fórmula general:
$$x=\frac{-(-3)\pm{}\sqrt{{(-3)}^2-4(1)(2)}}{2(1)}$$
$$x_1=\frac{3+\sqrt{1}}{2(1)}=\frac{3+1}{2}=2$$
$$x_2=\frac{3-\sqrt{1}}{2(1)}=\frac{3-1}{2}=1$$
Por lo tanto, la solución de la ecuación es:
$x_1=2$
$x_2=1$
2. Tenemos la siguiente ecuación cuadrática: ${4x}^2+12x+9=0$
Los coeficientes en este caso son $a=4$, $b=12$, $c=9$
$$x=\frac{-b\pm{}\sqrt{b^2-4ac}}{2a}$$
Sustituyendo los coeficientes en la fórmula general:
$$x=\frac{-(12) \pm \sqrt{(12)^2-4(4)(9)}} {2(4)}$$
$$x_1=\frac{12+\sqrt{0}}{8}=\frac{12}{8}=\frac{3}{2}$$
$$x_2=\frac{12+\sqrt{0}}{8}=\frac{12}{8}=\frac{3}{2}$$
Por lo tanto, la solución de la ecuación es:
$x_1=\frac{3}{2}$
$x_2=\frac{3}{2}$
3. Tenemos la siguiente ecuación cuadrática: $2x^2+x+3=0$
Los coeficientes en este caso son $a=2$, $b=1$, $c=3$
$$x=\frac{-b\pm{}\sqrt{b^2-4ac}}{2a}$$
Sustituyendo los coeficientes en la fórmula general:
$$x=\frac{-(1)\pm{}\sqrt{{(1)}^2-4(2)(3)}}{2(2)}$$
$$x_1=\frac{-1+\sqrt{-23}}{4}$$
$$x_2=\frac{-1-\sqrt{-23}}{4}$$
Como el resultado presenta raíces negativas, no tiene una solución en los números reales.
Lee atentamente cada pregunta, si es necesario resuelve la operación en tu cuaderno y luego elige la respuesta que consideres correcta.
-
- 7
- 5
- 9
- -3
La respuesta correcta es 5 porque se expande la expresión y se agrupa para encontrar los parámetros de la fórmula general de segundo grado:
$$(x–3)(x+2)+5=0$$
$$(x^2–3x+2x-6)+5=0$$
$$(x^2–x-6)+5=0$$
$$x^2–x-1=0$$
Los parámetros de la ecuación son: $a=1$, $b=-1$ y $c=-1$, el cálculo del discriminante es:
$$d={(-1)}^2-4(1)(-1)=1+4=5$$
-
- 7
- 5
- 9
- -3
La respuesta correcta es -3 porque se expande la expresión y se agrupa para encontrar los parámetros de la fórmula general de segundo grado:
$$(x+3)(x+2)+1=0$$
$$(x^2+3x+2x+6)+1=0$$
$$(x^2+5x+6)+1=0$$
$$x^2+5x+7=0$$
Los parámetros de la ecuación son: $a=1$, $b=5$ y $c=7$, el cálculo del discriminante es:
$$d={(5)}^2-4(1)(7)=25-28=-3$$
-
- 1
- -4
- 0
- -2
La respuesta correcta es 0 porque se expande la expresión y se agrupa para encontrar los parámetros de la fórmula general de segundo grado:
$$(x-3)(x+3)+9=0$$
$$(x^2-3x+3x-9)+9=0$$
$$(x^2-9)+9=0$$
$$x^2=0$$
Los parámetros de la ecuación son: $a=1$, $b=0$ y $c=0$, el cálculo del discriminante es:
$$d={(0)}^2-4(1)(0)=0-0=0$$
-
- Siempre es mayor que cero
- Siempre es igual a cero
- Siempre es menor que cero
- Puede tomar cualquier valor
Por la forma de la ecuación las soluciones son $x_1=0$ y $x_2=r$, por definición para tener dos soluciones reales el valor del discriminante debe ser positivo. Comprobando a través de la fórmula general:
$$x(x-r)=0$$
$$x^2-rx=0$$
Los parámetros de la ecuación son: $a=1$, $b=r-$ y $c=0$; el cálculo del discriminante es:
$$d=r^2-4(-r)(0)=r^2+0=r^2$$
-
- Siempre es mayor que cero
- Siempre es igual a cero
- Siempre es menor que cero
- Puede tomar cualquier valor
Por la forma de la ecuación, las soluciones son iguales, son $x_1=x_2=r$. Por definición, para tener dos soluciones iguales, el valor del discriminante es cero. Comprobando a través de la fórmula general:
$${(x-r)}^2=0$$
$$x^2-2rx+r^2=0$$
Los parámetros de la ecuación son: $a=1$, $b=-2r$ y $c=r^2$, el cálculo del discriminante es:
$$d={(2r)}^2-4(1)(r^2)={4r}^2-{4r}^2=0$$
-
- El discriminante es cero
- El discriminante es mayor que cero
- El discriminante es menor que cero
La trayectoria no toca ni atraviesa el eje x por lo tanto no tiene solución en los números reales y el discriminante es menor que cero.
-
- El discriminante es cero
- El discriminante es mayor que cero
- El discriminante es menor que cero
La trayectoria del atleta alcanza dos veces la horizontal (una al subir y otra al bajar), por lo tanto tiene dos soluciones y el discriminante debe ser mayor que cero.
-
- El discriminante es cero
- El discriminante es mayor que cero
- El discriminante es menor que cero
La trayectoria del atleta alcanza sólo una vez (una vez en el punto más alto), por lo tanto tiene dos soluciones iguales (solución “única”) y el discriminante debe ser cero.
1. ¿Cuánto vale el discriminante de la siguiente ecuación? $(x–3)(x+2)+5=0$
2. ¿Cuánto vale el discriminante de la siguiente ecuación? $(x+3)(x+2)+1=0$
3. ¿Cuánto vale el discriminante de la siguiente ecuación? $(x-3)(x+3)+9 = 0 $
4. Para las ecuaciones cuadráticas de la forma $x(x-r)=0$, se puede afirmar del discriminante que:
5. ¿Qué valores puede tomar el discriminante en ecuaciones basadas en un binomio cuadrado perfecto ${(x-r)}^2=0$?
6. Un atleta que realiza saltos de altura quiere imponer una nueva marca, sin embargo, se puso una meta muy ambiciosa y no alcanza la línea de salto. Considerando que barra horizontal corresponde al eje x y que la trayectoria del salto corresponde a una función de segundo grado, podemos afirmar que:
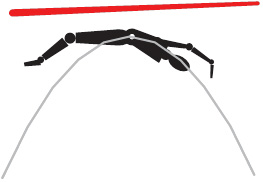
7. Un atleta que realiza saltos de altura quiere imponer una nueva marca. Considerando que barra horizontal corresponde al eje x y que la trayectoria del salto corresponde a una función de segundo grado, y logra brincar sobre la línea de salto, podemos afirmar que:
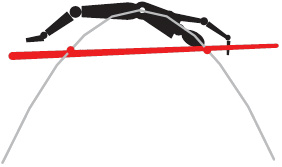
8. Un atleta que realiza saltos de altura quiere imponer una nueva marca Considerando que barra horizontal corresponde al eje x y que la trayectoria del salto corresponde a una función de segundo grado, si golpeara la barra de la línea de salto justo cuando alcanza el punto más alto, podemos afirmar que:
