Con base en la figura Razón de oro, el punto C divide al segmento $ \bar{AB} $ en “media y extrema razón” cuando la parte mayor de esta división, el segmento $ \bar{AC} $, es media proporcional entre el segmento total $ \bar{AB} $, y el segmento de la parte menor $ \bar{BC} $, es decir, en la proporción $\frac{AB}{AC}=\frac{AC}{CB}$, el segmento $ \bar{AC} $ se le llama media proporcional de los segmentos $ \bar{AB} $ y $ \bar{BC} $ y se le conoce como el “segmento áureo del segmento $ \bar{AB} $”.
La razón de oro $(Ø)$, es el número irracional que proviene del segmento áureo $ \bar{AC} $, por lo que satisface la proporción $\frac{AB}{AC}=\frac{AC}{CB}$. A las razones que la forman se les conoce como la razón de oro.
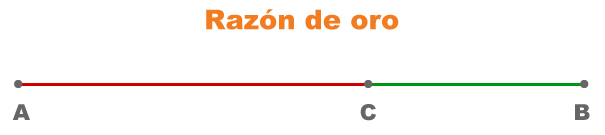
Para familiarizarte con la razón de oro, considera la longitud de los segmentos $AB=12$, $AC=7.41641$, $CB=4.58359$ y obtengamos su valor. $\frac{AB}{AC}=\frac{12}{7.41641}=1.61803$, y $\frac{AC}{CB}=\frac{7.41641}{4.58359}=1.61803$, por lo que la razón de oro es $Ø=1.61803$ tomando cinco decimales.
Ahora se generaliza la razón de oro, considerando la longitud de los segmentos $AC=x$, $CB=1$ y $AB=x+1$. Cabe mencionar que no se pierde generalidad para determinar el valor de la razón áurea y en cambio, facilita la operatividad algebraica.
Por ser AC el segmento áureo del segmento AB satisface la proporción $\frac{x+1}{x}= \frac{x}{1}$, como en toda proporción el producto de los términos medios es igual al producto de los términos extremos, se obtiene la ecuación cuadrática $ x+1=x^2$, y al agrupar sus términos al lado derecho de la ecuación resulta $x^2-x-1=0$, recordemos que al pasar un término al lado derecho o al lado izquierdo de la ecuación, se le suma el simétrico y se simplifica la ecuación. Al resolver la ecuación cuadrática con la fórmula general, se obtiene $ x=\frac {1+ \sqrt {5}}{2}=1.61803$.
Procedimiento
Fundamentación
$x^2-x-1=0$
Ecuación cuadrática, donde a es el coeficiente del término cuadrático $x^2$, b el coeficiente de término lineal x y c, término independiente
$ x = \frac {-(b) \pm \sqrt {(b)^2 - 4(a)(c)} } { 2(a) } $
Fórmula general, en ésta $a=1$, $b=-1$ y $c=-1$
$ x = \frac {-(-1) \pm \sqrt {(-1)^2 - 4(1)(-1)} } { 2(1) } $
Sustitución de a, b y c en la fórmula general
$ x = \frac {1 \pm \sqrt { 5 } } { 2 } $
Realización de operaciones y simplificar
$ x_1= \frac {1 + \sqrt { 5 } } { 2 } $, $x_2=\frac {1 - \sqrt { 5 } } { 2 }$
Soluciones de la ecuación cuadrática
$ x=\frac {1+ \sqrt {5}}{2}=1.61803$
Considerar a $x_1$ por ser positiva, ya que $x_2$ es negativa y carece de sentido en el contexto del problema
Al número irracional obtenido $ x=\frac {1+ \sqrt {5}}{2}=1.61803=ϕ$, se le conoce como la razón de oro y tiene múltiples aplicaciones, entre éstas, la construcción del rectángulo y la espiral de oro que se muestran a continuación.