Tiro parabólico
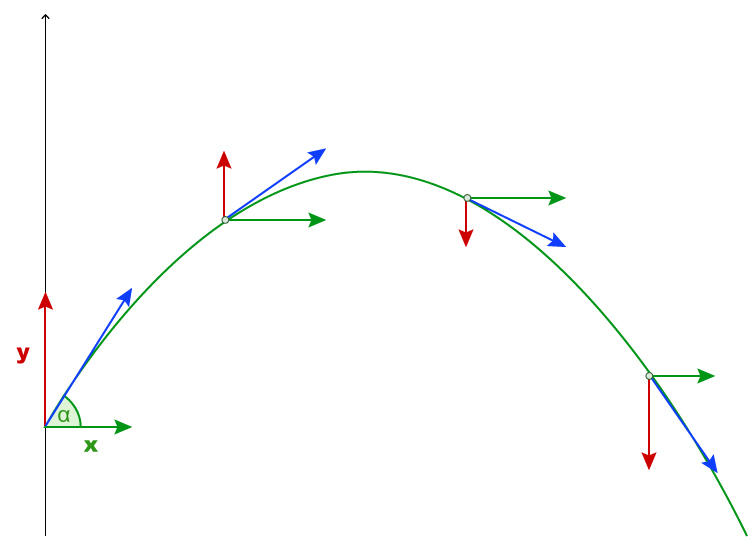
En la trayectoria del tiro parabólico, el vector x, representa a la componente horizontal con velocidad constante, mientras que el vector y, representa a la componente vertical con velocidad variable debido a la aceleración de la gravedad; con base en la figura de tiro parabólico se aprecia que la componente horizontal en todo el recorrido de la trayectoria tiene velocidad constante puesto que no actúa otra fuerza que la modifique (movimiento rectilíneo uniforme), sin embargo, la componente vertical al ascender hasta su punto más alto va disminuyendo, siendo cero en su punto más alto, mientras que cuando desciende aumenta debido a la aceleración de la gravedad (movimiento rectilíneo uniformemente acelerado). El análisis del movimiento de tiro parabólico lo realizaremos en el plano cartesiano, para ello, consideraremos a la variable t para saber la posición del balón de basquetbol en cualquier tiempo, mediante las componentes del tiro parabólico. A la variable t se llama parámetro y a las componentes del tiro parabólico, ecuaciones paramétricas, puesto que dependen del
parámetro t.
Con base en el estudio que se han realizado sobre la mecánica de los cuerpos lanzados verticalmente hacia arriba, y libres en su ascenso de toda resistencia, la ecuación paramétrica de la componente horizontal es x=vcos(α)t, mientras que para la componente vertical es y=vsen(α)t−12gt2+H. En ambas ecuaciones v es la velocidad inicial que se le aplica a los cuerpos al ser lanzados al aire, α es el ángulo de dirección que lleva la velocidad, g es la aceleración de la gravedad y H es la altura desde que los cuerpos son lanzados sin considerar la resistencia del aire, en particular, el lanzamiento del balón.
El tiempo t=xvcos(α), se sustituye en la ecuación de la componente vertical, obteniéndose la parábola y=−0.26x2+1.79x+1.5, para α=60.83°, v=8.88ms, mientras que la ecuación paramétrica de la componente vertical es y=7.75t−4.9t2+1.5.
Al despejar el tiempo t de la ecuación de la componente horizontal y sustituirla en la ecuación de la componente vertical, se obtiene la ecuación de la parábola en coordenadas cartesianas, tal como se muestra en seguida:
Revisa el proceso dando clic en los números
(1) Ecuación paramétrica horizontal del tiro parabólico
x=vcos(α)t
Despejar el tiempo t de la ecuación (1)
t=xvcos(α)
(2) Ecuación paramétrica vertical del tiro parabólico
y=vsen(α)t−12gt2+H
Sustituir t en la ecuación (2)
y=vsen(α)xvcos(α)−12g(xvcosα)2+H
y=sen(α)xcos(α)−12g(xvcosα)2+HSimplificar vv=1
y=tan(α)x−12g(x2v2cos2α)+H
Considerar tan(α)=sen(α)cos(α) y desarrollar el cuadrado
y=tan(60.83°)x−12(9.8)(x2(8.88)2cos2(60.83°))+1.5
y=1.79x−0.26x2+1.5
Al realizar las operaciones da la Ecuación cartesiana de la parábola
Sustituir α=60.83°, v=8.88ms, H=1.5m y g=9.8ms2
De forma similar al sustituir α=60.83°, v=8.88ms y H=1.5m, en la ecuación paramétrica de la componente vertical y=vsen(α)t−12gt2+H, se obtiene y=(8.88)sen(60.83°)t−12(9.8)t2+1.5, al realizar las operaciones da la ecuación cartesiana y=7.75t−4.9t2+1.5, teniendo como variable independiente el tiempo t. Al asignar un valor particular a la variable dependiente y, se obtiene la ecuación cuadrática correspondiente, tal como, se ejemplificará en la solución del problema del basquetbolista a continuación.
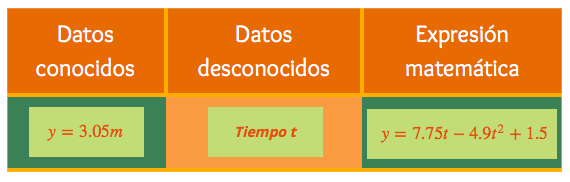
A partir de lo anterior arrastra a la tabla los datos conocidos y los desconocidos del problema, así como la ecuación vertical del tiro parabólico en su forma cartesiana, según correspondan. Las opciones correctas se marcarán en verde y las incorrectas en rojo.
- Tiempo t
- y=7.75t−4.9t2+1.5
- y=3.05m
| Datos conocidos | Datos desconocidos | Expresión matemática |
Cuando se sustituye y=3.05m en la ecuación y=7.75t−4.9t2+1.5, resulta la ecuación cuadrática 3.05=7.75t−4.9t2+1.5, que al escribirla en la forma ax2+bx+c=0, resulta 0=−4.9t2+7.75t−1.55, pasando 3.05 al lado derecho de la ecuación con el signo contrario y simplificando.
Con esta información ahora utiliza el método de tabulación para resolver la ecuación, también puedes apoyarte con el escenario de trabajo de Geogebra cuando se logra el enceste a la canasta. Escribe el valor del tiempo que calculaste en el recuadro y cuando termines da clic en Verificar para recibir retroalimentación.