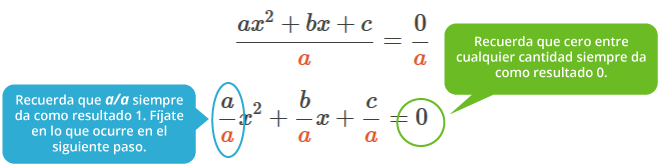
El siguiente paso es completar el trinomio cuadrado perfecto del lado izquierdo de la ecuación. Para ello, el término independiente c/a se resta en ambos lados de la ecuación para mantener la igualdad:

$x^2+\frac{b}{a}x+\frac{c}{a}-\frac{c}{a}=0-\frac{c}{a}$

simplificando $x^2+\frac{b}{a}x=-\frac{c}{a}$

Para completar el trinomio cuadrado perfecto del lado izquierdo de la ecuación:

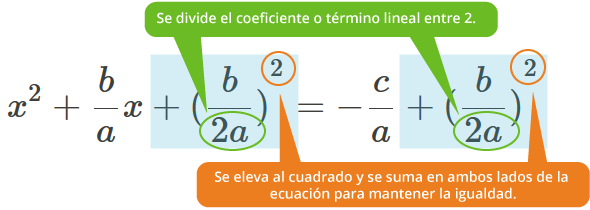
Ahora debemos factorizar el lado izquierdo de la ecuación. El resultado es el siguiente:

$${(x+\frac{b}{2a})}^2=-\frac{c}{a}+{(\frac{b}{2a})}^2$$

Al simplificar el término cuadrático del lado derecho, la ecuación queda así:

Para despejar a $x$, se obtiene la raíz cuadrada de ambos lados de la ecuación:

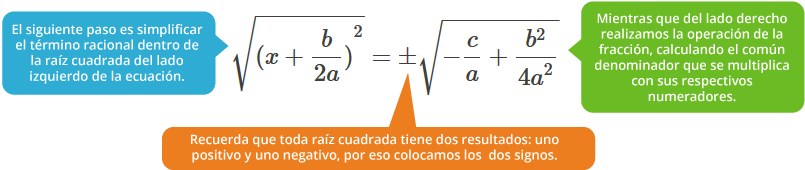
El resultado es el siguiente:

$$x+\frac{b}{2a}=\pm{}\sqrt{\frac{-4ac+b^2}{4a^2}}$$

Luego aplicamos el radical en el numerador y el denominador del lado derecho de la ecuación:

Luego debemos terminar el despeje de la variable $x$. Para ello hay que restar el término $\frac{b}{2a}$ en ambas partes de la ecuación:

$$x+\frac{b}{2a}-\frac{b}{2a}=\frac{\pm{}\sqrt{b^2-4ac}}{2a}-\frac{b}{2a}$$ $$x=\frac{\pm{}\sqrt{b^2-4ac}}{2a}-\frac{b}{2a}$$

simplificando

El signo $\pm{}$ quiere decir que hay dos soluciones, una con + y otra con -, es decir:

$$x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}$$ $$x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}$$