Problema viaje

Los problemas abordados con anterioridad hacen referencia a problemas de áreas. Para mostrar otros campos de aplicación de las ecuaciones cuadráticas, a continuación se presentan problemas relacionados con el cálculo de costos.

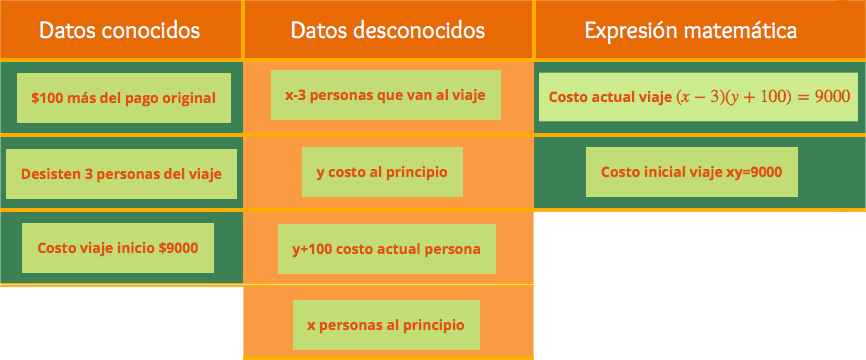
Problema. El transporte para una excursión con x personas tiene un costo de 9000. El costo por persona para el viaje es y pesos, si desisten tres personas, cada una de las personas restantes tendría que pagar 100 más. Obtén el número de personas que van a la excursión y determina la cantidad que paga cada una.

Instrucciones

Con base en el problema propuesto, identifica los datos conocidos, desconocidos y la relación entre ellos, mediante una ecuación de segundo grado. Arrástralos a los recuadros de la tabla según corresponda.

Arrastra

Costo viaje inicio $9000
x personas al principio
Desisten 3 personas del viaje
y+100 costo actual persona
Costo inicial viaje xy=9000
$100 más del pago original
x-3 personas que van al viaje
y costo al principio
Costo actual viaje $(x-3)(y+100)=9000$

Datos conocidos	Datos desconocidos	Expresión matemática

Las opciones correctas se han marcado en color verde, las incorrectas en color rojo.

Respuestas correctas:

Luego de establecer la relación entre datos, hay que obtener la ecuación cuadrática. A continuación se muestra cómo.

$xy=9000$ (1)

Ecuación costo viaje

$(x-3)(y+100)=9000$ (2)

Ecuación costo viaje al desistir 3 personas

$y= \frac{9000}{x}$

Despejar y de la ecuación 1

$(x-3)(\frac{9000}{x}+100)=9000$ (3)

Sustituir y en la ecuación 2

$(x-3)(\frac{9000}{x})+100(x-3)=9000$

Eliminar segundo paréntesis. Cada uno de sus términos se multiplica por (x – 3)

$(x)[(x-3)(\frac{9000}{x}) +100(x-3)=9000]$

Multiplicar por x a la ecuación para eliminar la x del denominador

$x(x-3)(\frac{9000}{x})+100x(x-3)=9000x$

Eliminar el corchete. Cada expresión en éste, se multiplica por x

$(x-3)(9000)+100x(x-3)=9000x$

Resultado al considerar $\frac {x}{x}=1$

$9000x-27000+100x^2-300x=9000x$

Eliminar los paréntesis

$9000x-27000+100x^2-300x-9000x=9000x-9000x$

Restar 9000x a los lados de la ecuación

$100x^2-300x-27000=0$

Ecuación cuadrática, obtenida al simplificar los lados de la ecuación

$x^2-3x-270=0$

Dividir la ecuación entre 100 para reducirla y facilitar la solución

Recuerda que la ecuación también puede resolverse utilizando la fórmula general, o mediante los métodos de factorización y de trinomio cuadrado perfecto.

Problema viaje

Problema viaje

Formulario de búsqueda