1. Inicio
  2. Matemáticas 2
  3. Unidad 1
  4. Problemas de aplicación
  5. Problema de Modelación 1

Problema de Modelación 1

Problema de Modelación cuadrática 1

Algunas relaciones entre las dimensiones de los cuerpos geométricos pueden establecerse mediante ecuaciones cuadráticas; las raíces de dichas ecuaciones permiten determinar longitudes desconocidas a partir de los datos conocidos. Para ello, analicemos el siguiente ejemplo: Se desea construir una caja con base cuadrada y sin tapa a partir de una lámina cuadrada en la que se harán cortes cuadrados de 3 decímetros en cada esquina. La caja toma forma cuando se doblan los lados de la lámina, tal como se muestra en la siguiente animación:

Haz clic en las tijeras para simular el corte de en las esquinas de la lámina; al hacerlo aparecerá un segundo ícono mediante el cual podrás simular el doblez de la lámina.

Ejercicio de Geogebra

Si la caja debe tener un volumen de 48 dm3 , ¿cuáles son las dimensiones que debe tener la lámina cuadrada para que cumpla con las condiciones descritas? ¿Cuál es el largo, ancho y alto de la caja?

A continuación veremos que las dimensiones de la lámina, y por lo tanto de la caja, se determinan mediante una ecuación cuadrática. Observa atentamente por qué.

Considerando que desconocemos la longitud de los lados de la lámina, entonces podemos identificar dicha longitud con la variable $x$, tal como se muestra en la imagen:

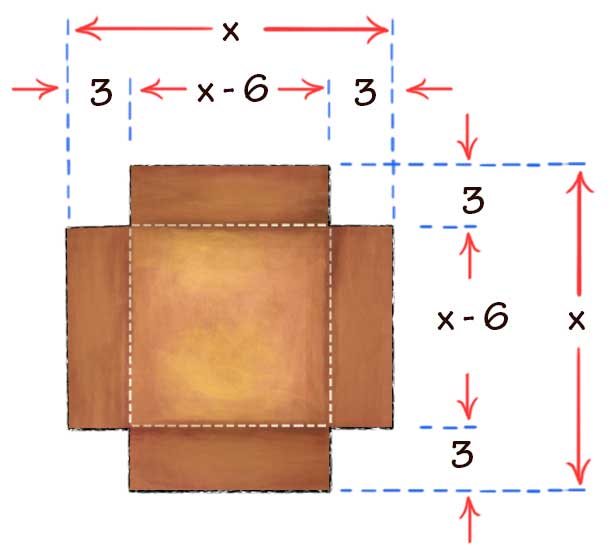
Modelación Cuadrática
Modelación Cuadrática
  1. Con base en la información proporcionada, completa el siguiente enunciado:

El área de la base de la caja es ( x-6 )2 y la altura es 3; así pues, la expresión para determinar el volumen $V$ de la caja está determinado por $V=$ 3( x-6 ) 2.

Como la caja debe contener un volumen de 48dm3, la expresión anterior queda como
3( x-6)2 = 48

Para poder verificar debes escribir en todos los espacios.
  1. Desarrolla y reordena los términos de la expresión anterior para obtener una ecuación cuadrática que relacione la longitud x de la lámina con el resto de las características indicadas en la animación. Introduce los coeficientes de la ecuación cuadrática en los espacios. Al finalizar haz clic en Verificar para recibir retroalimentación.

$x^2 - $ $x +$ $= 0$

Modelación Cuadrática
$$x^2-12x+20=0$$

Si partimos de la expresión:

$48=3(x-6)^2$ (ecuación 1)

Lo primero que debemos hacer es dividir ambos lados de la ecuación entre 3, de donde se obtiene:

$16=(x-6)^2$ (ecuación 2)

El segundo paso es desarrollar el lado derecho de la ecuación:

$(x-6)^2=(x-6) (x-6)$ (ecuación3)

$(x-6)^2=x^2-6x-6x+36$ (ecuación4)

$(x-6)^2=x^2-12x+36$ (ecuación5)

La ecuación 2 se puede reescribir una vez que hemos desarrollado el lado derecho y queda como:

$16=x^2-12x+36$ (ecuación6)

El siguiente paso es reodenar y restar 16 en ambos lados:

$x^2-12x+36-16=16-16$ (ecuación7)

Finalmente, obtenemos la expresión cuadrática:

$$x^2-12x+20=0$$ (ecuación8)

Para poder verificar debes escribir en todos los espacios.
  1. Ahora resuelve la ecuación en tu cuaderno para determinar las dimensiones de la lámina. Indica el resultado final en el espacio en blanco y haz clic en Verificar.

Longitud de la lámina:

dm

Si partimos de la expresión:

$x^2-12x+20=0$

Lo primero que debemos hacer es seleccionar el método más adecuado para su solución. En este caso se resolvió por fórmula general y el resultado es el siguiente:

$x_1=2$; $x_2=10$

A partir de las raíces obtenidas se tienen dos posibles medidas para la longitud de la lámina: 2 y 10 dm. Sin embargo, parece evidente que la construcción de una caja con una lámina cuadrada de 2 dm por lado es inaceptable, ya que tan sólo el corte de las esquinas es de 3 dm; por tanto, la longitud de la lámina es de 10 dm.

Para poder verificar debes escribir en el espacio correspondiente.

arriba