En este material presentaremos otro método para la resolución de ecuaciones cuadráticas conocido como trinomio cuadrado perfecto (TCP). Describiremos y analizaremos la factorización para valores particulares de los parámetros a,b y c, así como su generalización de la ecuación cuadrática ax2+bx+c. Además, desarrollaremos el método de completar trinomios cuadrados perfectos para aquellos que no lo son, por lo que es pertinente comprender el concepto de factorización.
La factorización consiste en expresar un número o un objeto (por ejemplo, un polinomio) como el producto de otros objetos más pequeños llamados factores.
Por ejemplo, el número 30 se factoriza mediante la multiplicación de sus números primos, es decir 2∙3∙5; y el polinomio a2−b2 se factoriza en la multiplicación de los binomios conjugados (a+b)(a−b).
El objetivo de la factorización es simplificar las expresiones algebraicas para lograr hacer procedimientos más sencillos, es decir, si se tiene la fracción 30210 entonces es conveniente factorizarla en sus números primos, por lo que sería 2∙3∙52∙3∙5∙7; la factorización nos permite expresar la fracción original como 17, una fracción que es mucho más fácil de manejar.
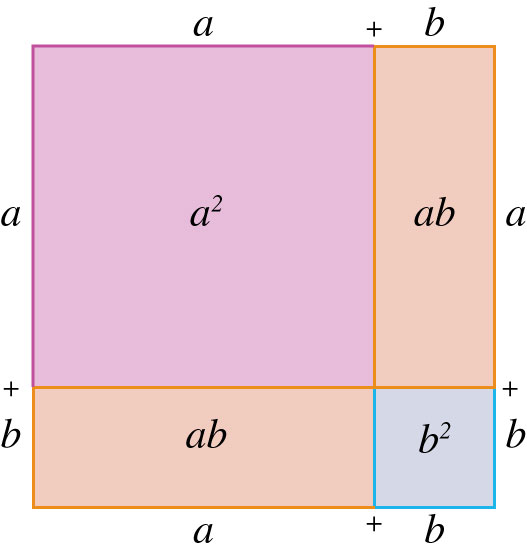
(a+b)2=a2+2ab+b2
De igual forma, factorizar un polinomio es expresarlo como el producto de sus factores con el fin de trabajar principalmente con los números enteros, motivo por el cual la factorización tiene gran importancia en muchas aplicaciones de la matemática, ya que permite formular expresiones complejas en términos más simples facilitando así su estudio y comprensión.
Con este material aprenderás a resolver ecuaciones cuadráticas mediante el método de completar el trinomio cuadrado perfecto, para modelar problemas que conduzcan a este tipo de ecuaciones.


