1. Inicio
  2. Matemáticas 2
  3. Unidad 1
  4. Problemas de aplicación
  5. Problema de Modelación 2

Problema de Modelación 2

Problemas de Modelación cuadrática

Un fabricante de termos desea realizar un cilindro recto con una altura de 20 centímetros y una capacidad de 620 cm3 como se muestra en la siguiente figura:

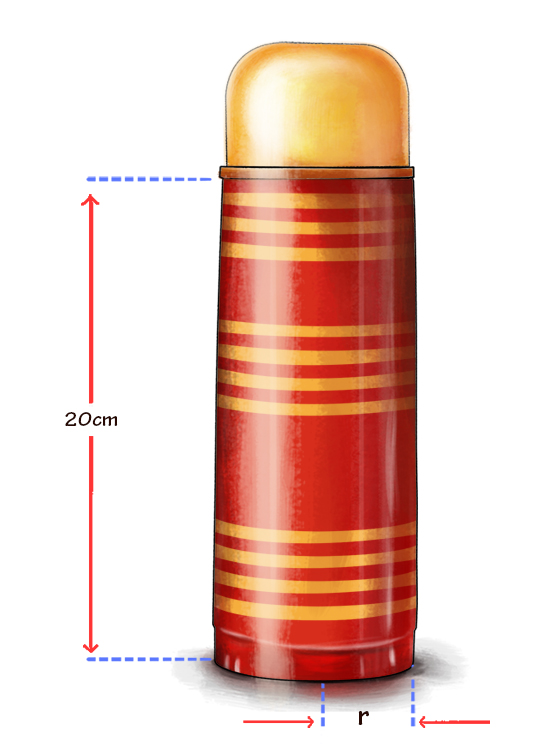
termo

Considerando que el volumen de un cilindro está determinado por la fórmula: $v=\pi r^2h $

  1. 1. ¿Cuál es el método de solución más pertinente para determinar el radio del termo para que contenga el volumen indicado (620 cm3)?
    • Fórmula general
    • Solución por factorización
    • Solución de la forma $ax^2+c=d$

    La forma más sencilla de obtener el radio es con la forma $ax^2+c=d$.

  1. Aplica en tu cuaderno el método que seleccionaste y escribe la solución con un decimal y la unidad de medida en el espacio en blanco. Al finalizar haz clic en Verificar para recibir retroalimentación.

El radio de la lata debe medir:

3.1 cm

Para determinar el radio interior de lata, dado un volumen de 620 cm3 y una altura de 20 cm, se sustituye en la expresión $v=\pi r^2h $ y se obtiene la siguiente ecuación cuadrática:

$620 = 20\pi {r^2}$

Para encontrar la raíz utilizaremos la solución de la ecuación del tipo $ax^2+c=d$, cuyo desarrollo es el siguiente:

Dividimos ambos lados de la ecuación entre $20\pi$

$\frac{{20\pi {r^2}}}{{20\pi }} = \frac{{620}}{{20\pi }}$

${r^2} = \frac{{620}}{{20\pi }}$

$r = \pm \sqrt {\frac{{620}}{{20\pi }}} $

Considerando que $\pi \approx 3.14$

$r \approx \pm \sqrt {\frac{{620}}{{20\left( {3.14} \right)}}} $

$r \approx \pm \sqrt {\frac{{620}}{{62.8}}} $

$r \approx \pm \sqrt {9.87} $

$r \approx \pm 3.1$

sus valores son

$r_1=-3.1$ cm

$r_2=3.1$ cm

Como las magnitudes negativas no tienen una interpretación física, entonces se concluye que el radio de la lata mide 3.1 cm.

Para poder verificar debes escribir en el espacio correspondiente.