Solución de la forma a(x+m)2=n
A continuación se muestran dos ejemplos específicos en los que se puede aplicar la solución de la forma a(x+m)2=n, da clic en las pestañas para revisar cada uno.
Solución de la ecuación 3(x−5)2=12
Esta ecuación se obtiene de la forma a(x+m)2=n, al sustituir los valores quedan de la siguiente manera:
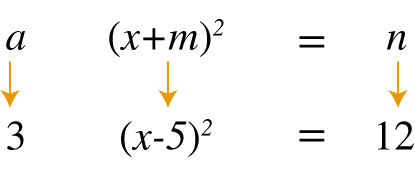
En este caso se despeja la incógnita x invirtiendo las operaciones que contiene la ecuación, aplicando las mismas operaciones que sean pertinentes a los dos lados de la ecuación para conservar la igualdad y obtener ecuaciones equivalentes cada vez más simples hasta llegar a la solución.
Revisa el proceso dando clic en los números
3(x−5)2=12
3(x−5)2=12
3(x−5)23=123
Para despejar el binomio cuadrado, se divide entre 3 ambos lados de la ecuación.
(x−5)2=4
Simplifica la ecuación.
3(x−5)2=12
3(x−5)23=123
(x−5)2=4
√(x−5)2=√4
Extraer la raíz cuadrada a los dos lados de la ecuación.
3(x−5)2=12
3(x−5)23=123
(x−5)2=4
√(x−5)2=√4
x−5=±2
Simplificar tomando los valores positivo y negativo de la raíz cuadrada.
3(x−5)2=12
3(x−5)23=123
(x−5)2=4
√(x−5)2=√4
x−5=±2
x−5+5=±2+5
Para despejar la variable x, se suman 5 a ambos lados de la ecuación.
x=±2+5
Se simplifica la ecuación.
x=2+5=7
x1=7
Solución 1, tomando el signo positivo.
x=−2+5=3
x2=3
Solución 2, tomando el signo negativo.
Comprobación
Para verificar que las soluciones encontradas son correctas, se sustituyen de la ecuación original 3(x−5)2=12 y se corrobora que se cumpla la igualdad:
Con x1=7
3(x−5)2=12
3(7−5)2=12
3(2)2=12
3(4)=12
12=12
Con x2=3
3(x−5)2=12
3(3−5)2=12
3(−2)2=12
3(4)=12
12=12
Como se cumple la igualdad, las soluciones encontradas son correctas.
Solución de la ecuación 23(x+4)2=5
Esta ecuación particular se obtiene de la forma a(x+m)2=n, con a=23, m=4 y n=5. En este caso es necesario despejar la incógnita x invirtiendo las operaciones, para obtener ecuaciones equivalentes cada vez más simples hasta llegar a la solución. Las soluciones encontradas son aproximadas.
Revisa el proceso dando clic en los números
23(x+4)2=5
23(x+4)2=5
23(x+4)223=523
Para despejar el binomio cuadrado, se divide entre 23 los dos lados de la ecuación.
(x+4)2=152
Se simplifica la ecuación.
23(x+4)2=5
23(x+4)223=523
(x+4)2=152
√(x+4)2=√152
Extraer la raíz cuadrada a los dos lados de la ecuación.
23(x+4)2=5
23(x+4)223=523
(x+4)2=152
√(x+4)2=√152
x+4=±√152
Simplificar tomando los valores positivo y negativo de la raíz cuadrada.
23(x+4)2=5
23(x+4)223=523
(x+4)2=152
√(x+4)2=√152
x+4=±√152
x+4−4=±2.738−4
Restar 4 a los dos miembros de la ecuación.
x=2.738−4=−1.261
x1=−1.261
Solución 1, tomando el signo positivo.
x=−2.738−4=−6.738
x2=−6.738
Solución 2, tomando el signo negativo.
Comprobación
Se sustituye cada una de las soluciones encontradas en la ecuación original 23(x+4)2=5 y verifica que se cumpla la igualdad:
Para x1=−1.261
23(x+4)2=5
23(−1.261+4)2=5
23(2.739)2=5
23(7.500)=5
5=5
Para x2=−6.738
23(x+4)2=5
23(−6.738+4)2=5
23(−2.739)2=5
23(7.500)=5
5=5
Como se cumple la igualdad, las soluciones encontradas son correctas.


