Generalización de la solución por factorización de una ecuación de segundo grado en su forma completa
Así pues, tenemos que de manera general para factorizar una ecuación de segundo grado se debe llevar a cabo el siguiente procedimiento.

ax2+bx+c=0
Si no es un trinomio cuadrado perfecto, entonces hay que buscar dos números a1 y a2 que multiplicados me den a y otros dos c1 y c2 que multiplicados me den c.
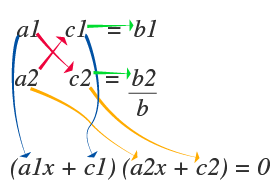
Una vez encontrados los valores que satisfacen el punto anterior, los colocamos de la siguiente manera, de tal forma que al multiplicar de forma cruzada y sumar estos valores nos dé como resultado el coeficiente del término lineal, o sea b.
Solo falta ordenar los términos encontrados en los paréntesis.
a1x+c1=0 a2x+c2=0
Aplicando la propiedad del producto nulo.
x1=c1a1 x1=c2a2
Despejando.



