Los fenómenos físicos se puede describir con múltiples modelos matemáticos, los cuales se ajustan con mayor o menor precisión al comportamiento real del fenómeno. Por ejemplo, el estudio del clima, su distribución y sus variaciones.
La temperatura sobre la superficie terrestre no es uniforme, pues presenta variaciones de temperatura en cada uno de los hemisferios y en las diferentes latitudes. Éstas también se pueden ajustar a modelos matemáticos que describen su comportamiento.
En la siguiente animación se muestra la variación de temperaturas en el hemisferio sur del planeta observa cómo cambian según la latitud.
Ahora analizaremos dos modelos matemáticos, uno lineal y uno cuadrático para ver cuál de ellos se ajusta a las mediciones indicadas. Éstos se encuentran conformados por:
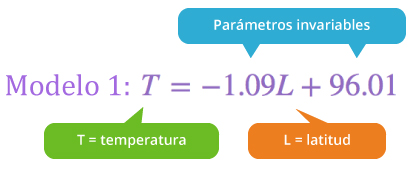
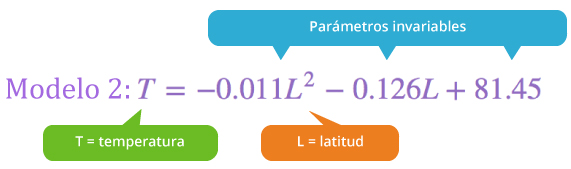
Por ejemplo, para una latitud de $85°S$, mediante el modelo lineal se obtiene el siguiente valor de temperatura:
$$T_1=-1.09(85)+96.01=3.4[°F]$$
Mientras que con el modelo cuadrático, considerando la misma latitud, se obtiene que la temperatura es:
$$T_2=-0.011(85)^2-0.126(85)+81.45=-8.7[°F]$$
Sin embargo, uno es estos modelos describe mejor la relación entre latitud y temperatura, para descubrirlo:
- 1. Completa la tabla que te presentamos a continuación. Para ello, determina las temperaturas correspondientes a las latitudes indicadas, utilizando las ecuaciones de los modelos lineal y cuadrático. Realiza las operaciones correspondientes en tu cuaderno y anota el resultado con un decimal en los espacios en blanco de la tabla. Cuando termines haz clic en el botón Verificar.
- Observa y compara la columna de “Temperatura real” con las columnas “Modelo lineal” y “Modelo cuadrático”. Ahora observa atentamente la gráfica que aparece a continuación y contesta la pregunta: ¿Cuál es el modelo que se ajusta mejor a las temperaturas reales? Finalmente haz clic en Verificar para recibir retroalimentación.
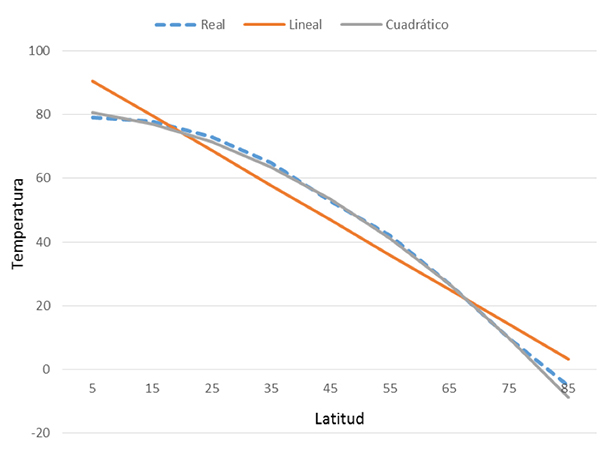
- A partir del modelo climático adecuado, realiza en tu cuaderno las operaciones correspondientes para determinar la latitud en el hemisferio sur en la que se presenta una temperatura anual promedio de 35°F. Introduce en la siguiente casilla el valor que obtuviste utilizando un decimal. Al finalizar haz clic en el botón Verificar.


