Factorización identificando si el trinomio es perfecto o no

Otra manera de resolver una ecuación cuadrática completa es mediante la identificación de sí ésta es o no, un trinomio cuadrado perfecto.
Resolver por factorización la ecuación:
x2+8x+16=0x2+8x+16=0
Nos damos cuenta que es un trinomio cuadrado perfecto. Sabemos que es perfecto cuando la raíz cuadrada del término cuadrático (1) y el término lineal (16) son números enteros.
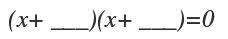
Colocamos los dos paréntesis y buscamos los valores que satisfagan la ecuación, es decir que multiplicados den 16 y sumados den 8.
(x+4)(x+4)=0
Factorizando como un binomio al cuadrado aquí mostrado en forma de factores.
x+4=0 x+4=0
Aplicando la propiedad del producto nulo.
x1=−4 x2=−4
Despejando.
Con un sencillo razonamiento se puede concluir que las ecuaciones cuadráticas que tienen la forma de un trinomio cuadrado perfecto tendrán dos soluciones iguales pues provienen de factores iguales, en este caso el 4.
Ahora, ¿qué pasará cuando nos encontramos con un trinomio cuadrado no perfecto como el siguiente?
Resolver por factorización la ecuación:
2x2+7x−4=0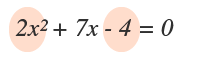
No es un trinomio cuadrado perfecto, porque la raíz cuadrada del término cuadrático (2) y el término lineal (7) deben ser números enteros y en este caso no lo son, entonces hay que buscar dos números que multiplicados den 2 y otros dos que multiplicados den 4
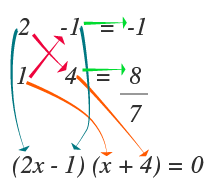
Una vez encontrados los valores que satisfacen el punto anterior, los colocamos de la siguiente manera, para que al multiplicar de forma cruzada y sumar estos valores nos dé como resultado el coeficiente del término lineal. En este caso para que la suma dé 7 debemos agregar un signo menos, pero los signos se agregan en la segunda columna.
Solo falta ordenar los términos encontrados en los paréntesis.
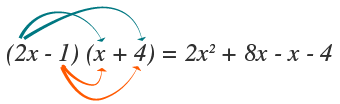
Antes de proceder a encontrar las soluciones hay que verificar si el producto de los binomios cumple con la ecuación original. Para ello se multiplica como lo indican las flechas.
(2x−1)(x+4)=2x2+7x–4
Ordenando términos.
2x−1=0 x+4=0
Aplicando la propiedad del producto nulo
x1=12 x2=−4
Despejando.



