1. Inicio
  2. Matemáticas 2
  3. Unidad 1
  4. Problemas de aplicación
  5. Problema de Modelación 3

Problema de Modelación 3

Problema de Modelación cuadrática 3

Un terreno rectangular que tiene dimensiones de 26 metros por 30 metros está rodeado por una banqueta de ancho uniforme desconocido (determinado por x). Si el área de la banqueta es de $A_T=240$ $m^2$ , ¿de cuánto es el ancho de la banqueta?

Para resolverlo considera que el área total de la banqueta $(A_T)$ es igual a la suma de sus partes ($A_1$ a $A_8$ ), es decir:

$A_T=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8$

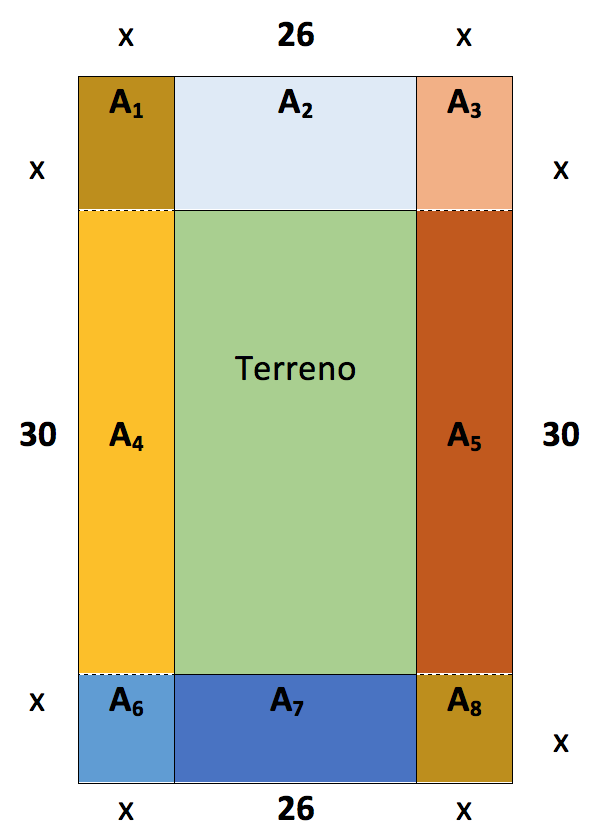
Modelación Cuadrática 3
  1. Arrastra los elementos lineales o cuadráticos que determinan el área de cada una de las partes de $(A_T)$. Obtén los datos del esquema del terreno. Al finalizar haz clic en Verificar para recibir retroalimentación.
  • $26x$
  • $30x$
  • $30x$
  • $26x$
  • $x^2$
  • $x^2$
  • $x^2$
  • $x^2$
$A_1=x^2$     $A_2=26x$    $A_3=x^2$    $A_4=30x$    $A_5=30x$     $A_6=x^2$    $A_7=26x$      $A_8=x^2$

Las opciones incorrectas se han marcado en color rojo.
  1. Por lo tanto, el área total de la banqueta expresada en términos del ancho de la banqueta $(x)$ es
$A_T=26x+26x+30x+30x+x^2+x^2+x^2+x^2$

donde $A_T=240m^2$

Determina la ecuación cuadrática que relaciona el área total de la banqueta con su ancho, simplicándola lo más posible e igualándola a cero. Escribe en el espacio en blanco y al finalizar haz clic en Verificar para recibir retroalimentación.

$x^2$

$=0$

$$26x+26x+30x+30x+x^2+x^2+x^2+x^2=240$$

$$4x^2+112x=240$$

$$4x^2+112x-240=240-240$$

$$4x^2+112x-240=0$$

Para simplificar la ecuación cuadrática anterior se deben dividir todos los elementos de la ecuación entre 4, valor que corresponde al máximo común divisor de todos los coeficientes:


$\frac{4}{4}{x^2} + \frac{{112}}{4}x - \frac{{240}}{4} = \frac{0}{4}$

La ecuación finalmente quedará así:

$$x^2+28x-60=0$$

Para poder verificar debes escribir en el espacio correspondiente.
  1. Ahora resuelve en tu cuaderno la ecuación para, finalmente, contestar la pregunta ¿De cuánto es el ancho de la banqueta? Escribe tu resultado y la unidad de medida en el espacio en blanco. Al finalizar haz clic en Verificar para recibir retroalimentación.

El ancho de la banqueta es de:

Las raíces de esta ecuación cuadrática corresponden a las posibles longitudes para el ancho de la banqueta con las dimensiones indicadas en el problema. Tales raíces se encuentran utilizando los métodos Factorización o Fórmula general y sus valores son

$$x_1=2$$

$$x_2=-30$$

Como las magnitudes negativas no tienen una interpretación física, entonces se concluye que el ancho de la banqueta mide $2 m$.

Para poder verificar debes escribir en el espacio correspondiente.

arriba

Para saber más

Revisa el material Fórmula general para repasar el método de resolución de este problema.
Revisa el material Solución por factorización para repasar el método de resolución de este problema.