Solución por factorización de ecuaciones cuadráticas en su forma completa
Las ecuaciones cuadráticas tienen por lo común dos fuentes de origen:
problemas concretos de la vida real o personas que las producen de manera abstracta.
Tratándose de utilidad, las ecuaciones cuadráticas tienen muchas aplicaciones y en diferentes ámbitos. Algunos ejemplos son los siguientes:
El uso de ecuaciones cuadráticas en la ingeniería está ampliamente relacionado con cualquiera de sus áreas, ya que es un concepto matemático básico que ayuda a resolver una gran cantidad de problemas. En la ingeniería civil, por ejemplo, es usada en gran medida en la construcción de diseños parabólicos o curvos tales como sistemas de carreteras, ferrocarriles, puentes, canales, proyectos de riego, etc.

Los astrónomos usan ecuaciones cuadráticas para describir las órbitas de los planetas, sistemas solares y galaxias. Los físicos las usan para detallar los diferentes tipos de movimiento. Incluso los químicos las necesitan para describir ciertos tipos de reacciones químicas.
El uso más común que se le da a las ecuaciones cuadráticas dentro de la agricultura es la optimización del área en donde se desee hacer una cosecha, es decir, se resuelven problemas para hacer uso de la mayor cantidad de suelo posible con el menor gasto de materiales.

Hasta el momento sabemos lo siguiente:
La expresión ax2+bx+c=0 se denomina forma general de la ecuación cuadrática, donde x es la incógnita. Los nombres de cada elemento son:
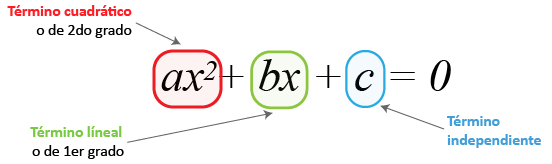
Para que exista la ecuación cuadrática es necesario que el coeficiente a≠0 de lo contrario, el término cuadrático faltaría y con él la ecuación cuadrática. En la ecuación completa a,b,c tienen que ser diferentes de cero.
Algunos ejemplos de este tipo de ecuaciones son las siguientes:
5r2+12r+4=0
2m2+10m−48=0
x2−3x−40=0
En los primeros dos ejemplos se consideran “r” y “m” las incógnitas.
Pero, ¿qué es factorizar?
Hay que recordar que los términos que conforman una multiplicación se llaman factores.
Por ejemplo:
En la multiplicación 2 x 3 x 5=30, los números 2, 3 y 5 son factores de 30.
En el caso de una expresión algebraica, los factores son términos algebraicos que se multiplican entre sí.
Por ejemplo: 2x(x+3)(x−2)
Aquí se muestra la multiplicación de cuatro términos: 2, x, (x+3) y (x−2), los cuales son factores.
Esto significa que factorizar una expresión algebraica, consiste en transformarla de manera que se vea como una multiplicación de términos.
Una buena cantidad de ecuaciones cuadráticas de este tipo pueden resolverse de forma inmediata por factorización cuando sean productos notables.



