Si dos o más números racionales tienen igual denominador, entonces es mayor la fracción que posee el numerador mayor.

Por ejemplo, al comparar $\frac{4}{9}$ y $\frac{1}{9}$ se observa que ambas fracciones corresponden a unidades que han sido divididas en $9$ partes iguales. Sin embargo, el numerador de la primera fracción indica que se han tomado $4$ partes; mientras que el numerador de la segunda fracción indica que se ha tomado una parte. Lo anterior se ilustra en la figura, en donde se muestra que es mayor la fracción con el numerador mayor.

 

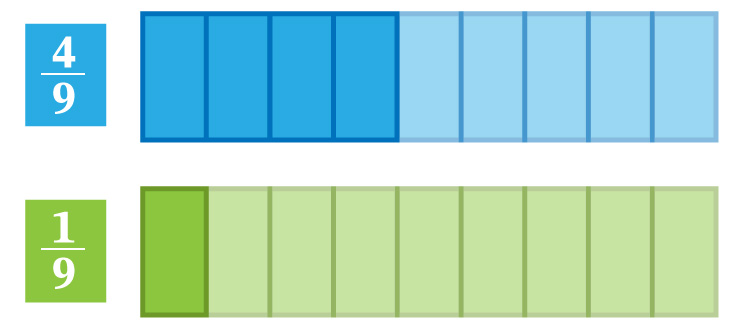
Por lo tanto, $\frac{4}{9}$ es mayor que $\frac{1}{9}$ ya que tienen el mismo denominador ($9$) y el numerador del primer número es mayor que el del segundo; es decir

$\frac{4}{9} > \frac{1}{9}$

 

 

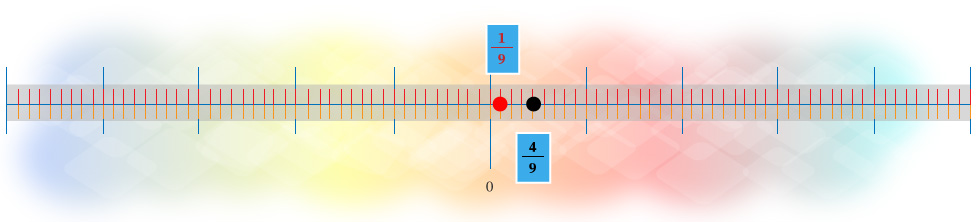
Ejemplo

Determinar el orden de los números $-\frac{43}{9}$ y $-\frac{3}{9}$

Como los números tienen el mismo denominador ($9$), entonces se deben comparar los valores de los numeradores: $-43$ y $-3$; se tiene que $-43 < -3$, por lo tanto:

$\frac{-43}{9} < \frac{-3}{9}$

 

 

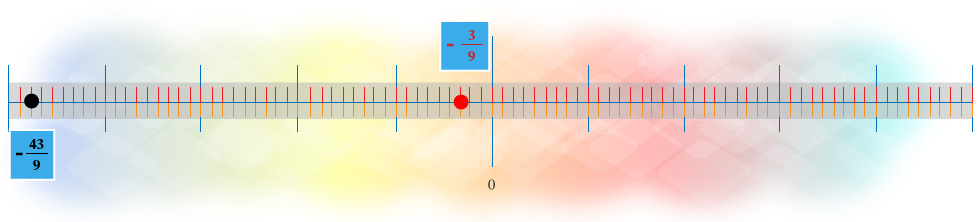
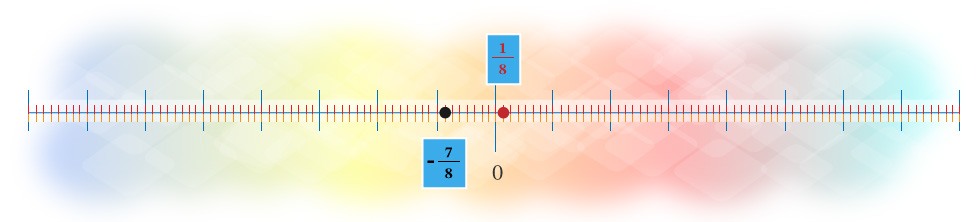
Ejemplo

Determinar el orden de los números $-\frac{7}{8}$ y $\frac{1}{8}$

Como los números tienen el mismo denominador ($8$), entonces se deben comparar los valores de los numeradores:$-7$ y $1$; se tiene que $-7 < 1$, por lo tanto

$\frac{-7}{8} < \frac{1}{8}$

 

Esta misma conclusión se obtiene por la diferencia de signos, ya que las fracciones positivas son mayores que las negativas.