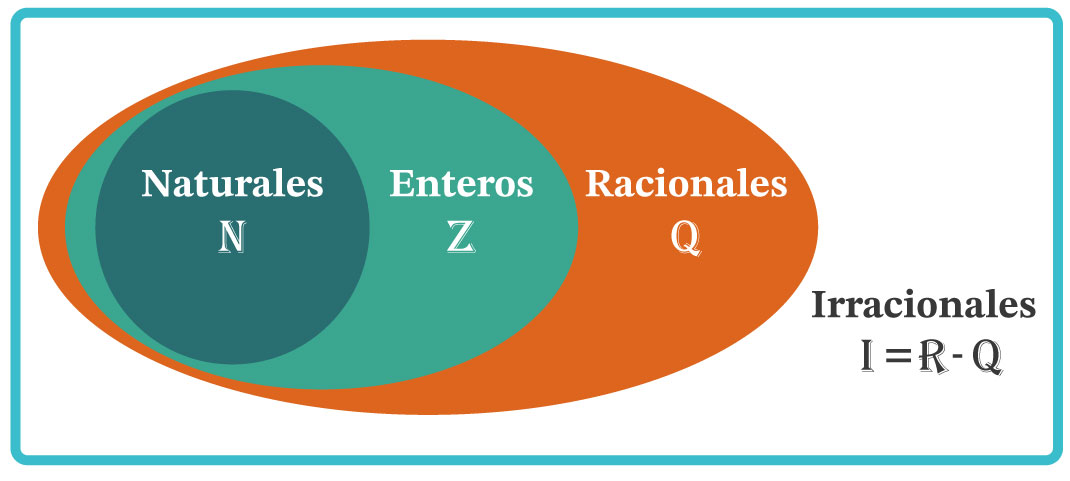
Los números racionales son una extensión de los números enteros, surgen como una necesidad de realizar representaciones de partes o fracciones de algo. Inicialmente se utilizaron para describir el inverso multiplicativo de un número entero. También se usaron para obtener partes iguales de algún producto cuando se realizaban trueques, repartir porciones de alimento, dividir terrenos o el tiempo para ubicarnos en algún momento del día. Al introducir el concepto de la división, se genera el conjunto de los números racionales, que se definen como el cociente de dos números enteros. Al igual que se representa a los números naturales con N y a los enteros con Z, se utilizó la letra Q (quotient, “cociente” en varios idiomas) para representar a los números racionales.
El conjunto de los números racionales, se definen como el cociente ab, donde a y b son números enteros y b≠0

Algunas observaciones sobre el cociente ab:
- b no puede tomar el valor de cero porque la división quedaría “no definida”.
- Los números enteros son parte de los números racionales, con b=1.
- Cuando a=1, quedan fracciones que no pueden reducirse a otra fracción y representan una parte igual de un todo: la mitad (12), un tercio (13), un cuarto (14), etc.
Los números enteros son un subconjunto de los números racionales (donde el denominador es igual a 1), por lo que:
Desde el punto de vista de las expresiones matemáticas, en algún momento fue necesario representar la división; es así como surgen los números racionales. Por ejemplo, al plantearse expresiones como dividir dos pizzas entre cinco personas se tiene que:

Practicando
Ahora responde la siguiente pregunta escribiendo en el espacio correspondiente tu resultado. Al finalizar haz clic en Verificar para recibir retroalimentación.
Si se pagaron $250 por las dos pizzas, ¿cuánto pagará cada una de las personas si se dividen de manera igual el costo?
Los resultados de las divisiones no necesariamente serán número enteros, de ahí la necesidad de establecer nuevas representaciones.
Las fracciones son la primera aproximación hacia los números racionales, en ellas se representa la división de una cantidad entera (numerador) en partes iguales (denominador).
Se trata de una fracción propia cuando el numerador es menor que el denominador, es decir, cuando el resultado de esta división se encuentra entre cero y uno. Por ejemplo:
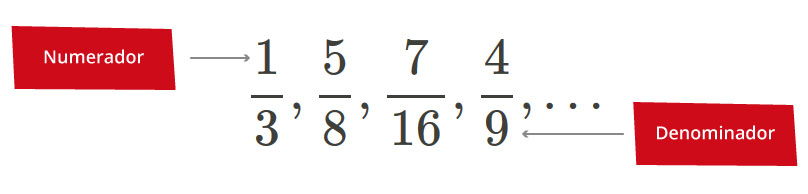
Si el numerador es mayor o igual que el denominador, se le conoce como una fracción impropia. En estos casos puede observarse que el resultado de la división es mayor o igual a 1. Por ejemplo:
33,85,167,149,…
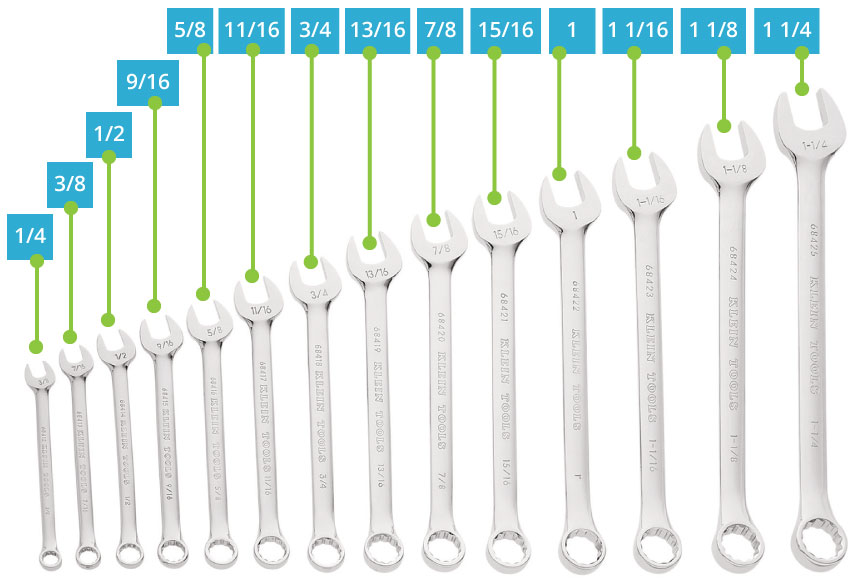
Las fracciones mixtas, son expresiones matemáticas que representan una fracción impropia como la suma de un entero más la suma de una fracción propia. Este tipo de notación es muy utilizado en el sistema de medición inglés. Por ejemplo, podrás encontrar llaves de 1/2, 3/4 o 1 pulgada, pero también de 11/4 de pulgada. Estas fracciones comunes suelen representarse con una diagonal separando al numerador del denominador 1/4=14.
Practicando
Ahora responde las siguientes preguntas escribiendo en el espacio correspondiente tu resultado. Al finalizar haz clic en Verificar para recibir retroalimentación.



