Hay problemas que involucran dos condiciones entre las cantidades conocidas y las que se desean conocer, por lo cual un sistema de dos ecuaciones lineales con dos incógnitas puede ser útil para resolver ese tipo de problemas, ya que cada ecuación expresa una condición.
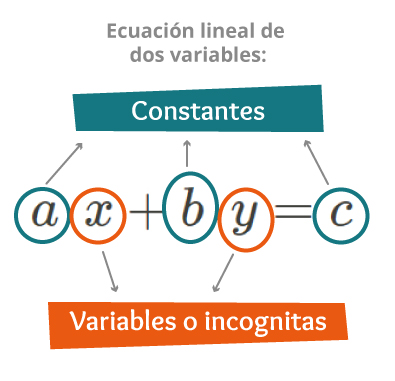
Una ecuación lineal de dos variables es de la forma ax+by=c, donde a,b y c son constantes, mientras que x, y son las variables o incógnitas. Por ejemplo, en la ecuación lineal 2x+3y=12 las constantes son a=2, b=3, c=12, mientras que x, y son las variables que pueden tener muchos valores y cada pareja de valores x, y que cumplen con la ecuación son una solución de ésta.
En un sistema de dos ecuaciones lineales con dos incógnitas puede tenerse una solución, ya que se deben cumplir las dos ecuaciones a la vez, aunque también llega a haber casos con infinidad de soluciones o con ninguna.
Entre los problemas que se pueden resolver con los sistemas de ecuaciones lineales están los de costos, los de precios de mercancías, de inversiones de dinero a ciertas tasas de interés, porcentajes en mezclas, partes de cantidades diversas, entre otros.
En este objeto de aprendizaje se plantea resolver sistemas de ecuaciones que tienen soluciones con diferentes características, enfatizando su relación con las soluciones gráficas a través de recursos GeoGebra y finalmente se propone resolver otros sistemas de ecuaciones y problemas.
Con este material aprenderás a resolver correctamente sistemas de ecuaciones lineales de dos variables por el método de suma o resta, para aplicarlo a la solución de problemas que se modelen con este tipo de sistemas.


