Si dibujas un cuadrado cuyos catetos son de tamaño 1, ¿cuál es la medida de su diagonal?
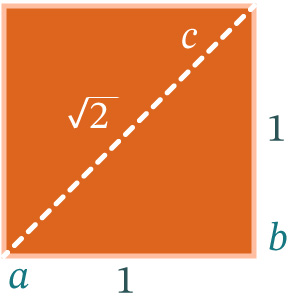
Recordando el Teorema de Pitágoras, sabemos que:
$c^{2}=a^{2}+b^{2}$
En donde:
$c= \sqrt{a^{2}+b^{2}}$
Sustituyendo los valores, tenemos que:
$c=\sqrt{1^{2}+1^{2}}=\sqrt{1+1}=\sqrt{2}=1.4142135623730950...$
Este número no puede ser expresado como el cociente de dos números enteros. Entonces, si no es un número racional, ¿qué es?, los números que no son racionales se le conocen como números irracionales.
Además de números como $\sqrt{2}$ , también se pueden mencionar otros números irracionales como $\pi$ (cociente de la longitud de la circunferencia entre su diámetro) o e (utilizado en situaciones que representan crecimiento o decrecimiento exponencial).
Si los representamos en la recta numérica sería de la siguiente forma:
Los números irracionales se representan con la siguiente letra
$\mathbb{I}$