Problemas aritméticos que involucren relaciones
A continuación se presentan problemas aritméticos que involucran una relación entre partes de una cantidad y la cantidad; estas relaciones se encuentran cuando dos magnitudes son directamente proporcionales, es decir, si al incrementarse o disminuir una de ellas, la otra lo hace en la misma proporción, lo que significa que una proporción es la igualdad de dos razones. En toda proporción el producto de los términos medios es igual al producto de los términos extremos (teorema fundamental de las proporciones). Esto se representa de la siguiente forma:
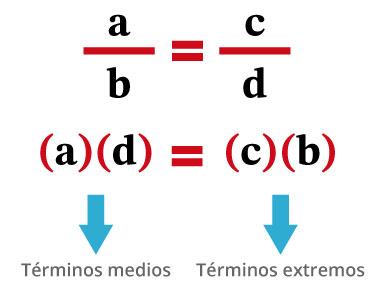
Esta es la propiedad que nos permite ver si dos cantidades son proporcionales verdaderamente.
Ahora revisa los siguientes ejemplos
Un saco de papas pesa 8 kg. ¿Cuánto pesan 7 sacos de papas?
Paso 1. Recabar los datos conocidos
1 saco de papas 8 kg
7 sacos de papas ¿Cuántos kg?
Paso 2. Realizar el procedimiento
Si aumento el número de sacos de papas aumenta el peso en kg, ordenando los datos:
1 -----> 8 kg
7 -----> x kg
Con la relación:
$$\frac{a}{b}=\ \frac{c}{d}\ \ entonces\ \ \left(a\right)\left(d\right)=(b)(c)$$
Resulta:
$$\frac{1}{7}=\ \frac{8}{x}\ \ entonces\ \ \left(1\right)\left(x\right)=(7)(8)$$
$$x=\frac{(7)(8)}{1}=56$$
Respuesta
7 sacos de papas pesan 56 kg
En 30 litros de agua de mar hay 750 gramos de sal. ¿Cuántos litros de agua de mar tendremos para obtener 5,000 gramos de sal?
Paso 1. Recabar los datos conocidos
En 30 litros de agua de mar hay 750 gramos de sal Para 5,000 gramos de sal ¿Cuántos litros de agua de mar?
Paso 2. Realizar el procedimiento
Si aumento el número de litros de agua de mar aumenta el peso en gramos de sal, ordenando los datos:
750 gramos de sal -----> 30 litros de agua de mar
5,000 gramos de sal -----> x litros de agua de mar
Con la relación:
$$\frac{a}{b}=\ \frac{c}{d}\ \ entonces\ \ \left(a\right)\left(d\right)=(b)(c)$$
Resulta:
$$\frac{750}{5000}=\ \frac{30}{x}$$
$$\left (750 \right )\left ( x \right )= \left ( 5000 \right )\left ( 30 \right ) $$
$$x=\frac{(5000)(30)}{750}=200$$
Respuesta
Se necesitan 200 litros de agua de mar para obtener 5000 gramos de sal
Un automóvil tenía un precio la semana pasada de 25,000.00, actualmente cuesta 5,000.00 más. ¿Cuál es el porcentaje de aumento?
Paso 1. Recabar los datos conocidos
Precio de antes 25,000.00
Actualmente cuesta 5,000.00 más ¿Cuál es el porcentaje?
Paso 2. Realizar el procedimiento
25,000.00 -----> 5,000.00
100% -----> x%
Con la relación:
$$\frac{a}{b}=\ \frac{c}{d}\ \ entonces\ \ \left(a\right)\left(d\right)=(b)(c)$$
Resulta:
$$\frac{25000}{100}=\ \frac{5000}{x}$$
$$\left (25000 \right ) \left ( x \right ) = \left ( 100 \right )\left ( 5000 \right ) $$
$$x=\frac{(100)(5000)}{25000}=20$$
Respuesta
El automóvil aumentó 20% más del precio de la semana pasada.
Al comprar un refrigerador en el departamento de línea blanca que cuesta 4,450.00 nos hacen un descuento del 8%. ¿Cuánto tenemos que pagar en la caja?
Paso 1. Recabar los datos conocidos
Precio del refrigerador 4,450.00
Descuento del 8% ¿Cuánto hay que pagar?
Paso 2. Realizar el procedimiento
4,450.00 -----> 100%
x -----> 8%
Con la relación:
$$\frac{a}{b}=\ \frac{c}{d}\ \ entonces\ \ \left(a\right)\left(d\right)=(b)(c)$$
Resulta:
$$\frac{4450}{x}=\ \frac{100}{8}$$
$$\left(4450\right)\left(8\right)=(x)(100)$$
$$x=\frac{(4450)(8)}{100}=\ 356$$
El descuento del 8% son 356.00
4,450.00 - 356.00 = 4,094.00
Respuesta
En la caja vamos a pagar por el refrigerador 4,094.00
Un automóvil que hará un viaje de la Ciudad de México a Mazatlán, Sinaloa debe recorrer una distancia 1,016 kilómetros, el automóvil tiene una eficiencia en el gasto de la gasolina de 20 kilómetros por cada litro, si el litro de gasolina cuesta 15.99 ¿Cuánto dinero gastará en combustible?
Paso 1. Recabar los datos conocidos
Distancia de la Ciudad de México a Mazatlán, Sinaloa = 1,016 kilómetros
Eficiencia en el gasto de la gasolina de 20 kilómetros por cada litro
El litro de gasolina cuesta 15.99
Paso 2. Realizar el procedimiento
20km -----> 1 litro
1,016 km -----> x litro
Con la relación:
$$\frac{a}{b}=\ \frac{c}{d}\ \ entonces\ \ \left(a\right)\left(d\right)=(b)(c)$$
Resulta:
$$\frac{20}{1016}=\ \frac{1}{x}$$
$$\left(20\right)\left(x\right)=(1016)(1)$$
$$x=\frac{(1016)(1)}{20}=\ 50.8$$
El automóvil va a gastar 50.8 litros de la Ciudad de México a Mazatlán, Sinaloa
Para el costo de la gasolina
$$Costo\ de\ la\ gasolina=(50.8)($ 15.99)=$812.29$$
Respuesta
El automóvil va a gastar la cantidad de 812.29 de la Ciudad de México a Mazatlán, Sinaloa.