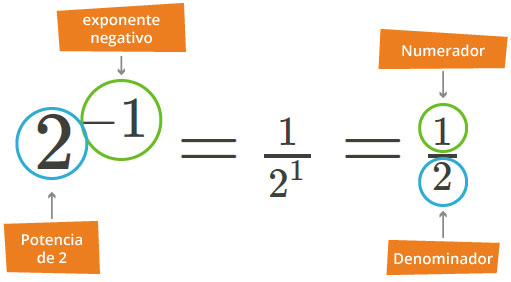Esta operación es fundamental en Matemáticas ya que te permitirá la resolución de problemas en biología, negocios, informática, ingeniería y física, entre otros campos de aplicación. Por lo que su estudio te facilitará la comprensión de sus conceptos involucrados y el descubrimiento de regularidades para la formulación de sus leyes, las cuales aplicarás en la simplificación de expresiones que involucran potencias y su aplicación en la resolución de problemas.
La potenciación es la operación que consiste en multiplicar el número llamado base por sí mismo las veces que indica el exponente. Para ilustrarlo revisa el siguiente recurso Geogebra que se te presenta. En éste la expresión (a)n es la potencia de la base a elevada al exponente n. Cabe señalar que el exponente para la potencia es un número natural.
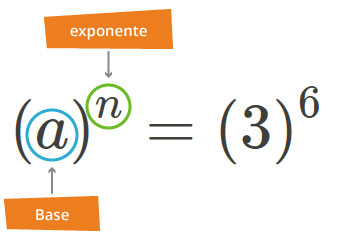
Da clic en Significado de las potencias para ir al recurso GeoGebra.
A manera de resumen se puede decir que:
- La potenciación es la operación que consiste en multiplicar el número llamado base por sí mismo las veces que indica el exponente.
- Cuando la base es negativa y el exponente par, la potencia es positiva, pero con exponente impar, la potencia es negativa.
- Cuando la base es positiva y el exponente es par o impar, la potencia es positiva.
Practicando
Para consolidar tu aprendizaje sobre las potencias que trabajaste con el recurso Geogebra, te presentamos una tabla en la que puedes ver algunos ejemplos de cómo se aplica esta ley, con base en éstos, obtén el último resultado y escríbelo en la casilla correspondiente. Al finalizar da clic en Verificar para recibir retroalimentación.
Ahora veamos qué ocurre cuando el exponente de la potencia es cero o negativo. Para ello, se te presenta una tabla con potencias de exponentes positivos, negativos e incluso cero, obsérvalas de derecha a izquierda para que comprendas su significado.
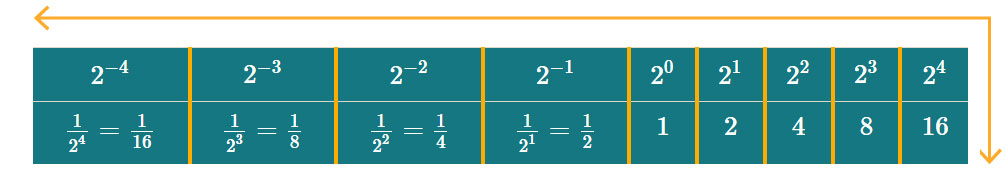
Al considerar la tabla de derecha a izquierda, observamos en el primer renglón que los exponentes de las potencias de 2 van disminuyendo en 1, mientras que en el segundo renglón el valor de la potencia disminuye a la mitad. Con base en esto llegamos a los siguientes resultados:
| 24=16 | 23=8 | 22=4 | 21=2 | 20=1 | |||||
| 2−1=121=12 | 2−2=122=14 | 2−3=123=18 | 2−4=124=116 | y así sucesivamente |
Por lo anterior se concluye lo siguiente:
- La potencia de 2 con exponente 0 es 1.
- La potencia de 2 con exponente negativo se representa como un cociente, cuyo numerador es 1 y denominador es la potencia de 2 con exponente positivo, tal como se pudo apreciar en los ejemplos.