Problemas de velocidad

Ahora toca abordar problemas de velocidad constante, los cuales involucran tiempo, distancia y velocidad como has aprendido en Física.

$velocidad = \frac{distancia}{tiempo}$

Por lo que: $distancia =Velocidad \times tiempo$

Generalmente encontrarás la distancia medida en kilómetros y el tiempo en horas.

Revisa los siguientes problemas de velocidad dando clic en cada una de las pestañas

Problema del viaje
Problema de la casa a Zapopan

Carolina viaja en su automóvil de Mazatlán a Culiacán con una velocidad promedio de 80 km/h. Una hora después sale una avioneta de Mazatlán hacia Culiacán siguiendo la ruta del automóvil y volando a 400 km/h. ¿Cuánto tarda la avioneta en alcanzar al automóvil?

Para este tipo de problemas también te puede ayudar si realizas un diagrama:

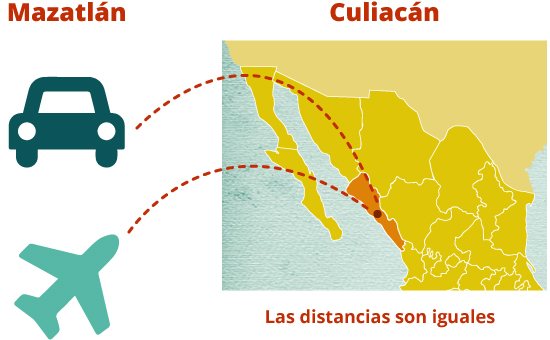
Sea $t$ el tiempo en horas que tarda la avioneta en volar la misma distancia que el carro.

	Tiempo [h]	Velocidad [km/h]	Distancia [km]
Automovil	$t+1$	$80$	$80(t+1)$	La avioneta sale una hora después, así que el automóvil viaja durante una hora más
Avioneta	$t$	$400$	$400t$

Ahora, completa los espacios correspondientes, empezando por la ecuación que plantea el problema, la cual se obtiene al considerar que las distancias son iguales. Al finalizar da clic en Verificar para recibir retroalimentación.

$($

$)=$

$80(t+1)=400t$

Propiedad distributiva:	$80t$ + $80$ = 400t
Resta $80$	$80t+80-80=400t-80$
Simplifica:	$80t=400t-$ $80$
Resta 400t	$80t-400t=400t-80-400t$
Simplifica:	-320t = -80
Divides entre -320	$\frac{-320t}{-320} = \frac{-80}{-320}$
Solución de la ecuación:	$t=$ $t=\frac{1}{4}$

En la solución de la ecuación obtuviste una fracción, la cual deberás indicar cuántos minutos corresponden para dar la solución al problema. Recuerda que una hora tiene 60 minutos.

Solución: La avioneta tarda quince minutos en alcanzar al automóvil.

Puedes verificar tu solución, sustituyendo en la ecuación que plantea el problema.

$80 \left ({\color{green}{\frac{1}{4}}} + 1 \right ) = 400 \left ({\color{green}{\frac{1}{4}}} \right )$

$80 \left ({\color{green}{\frac{5}{4}}} \right ) = {{\frac{400}{\color{green}4}}}$

$100=100$

arriba

Gonzalo sale de su casa para Zapopan que dista 604 kilómetros. Después de dos horas de camino tiene que reducir la velocidad en 30 km/h debido a la lluvia. Si durante el trayecto tardó una hora para comer y cargar gasolina, y llega a Zapopan nueve horas después de haber salido de su casa. ¿Cuál fue su velocidad durante las dos primeras horas de su viaje?

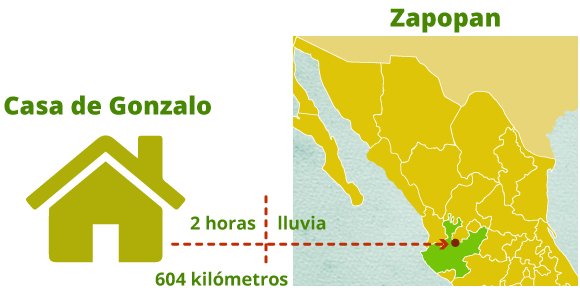
Sea $v$ la velocidad con la que inicia el viaje Gonzalo en km/h.

	Tiempo [h]	Velocidad [km/h]	Distancia [km]
Primer tramo	$2$	$\color{green} v$	${\color{Green} {2v}}$
Segundo tramo	$6$	${\color{Green} {v}}-{\color{Green} {30}}$	$6({\color{Green} {v}}-{\color{Green} {30}})$

Las horas para el segundo tramo se calculan como sigue: el tiempo total que tarda son nueve horas, menos dos horas del primer tramo, menos una hora parado porque comió y cargó gasolina; quedan seis horas para el segundo tramo que es el viaje durante la lluvia.

La ecuación que plantea el problema se obtiene considerando que hay 604 kilómetros de la casa de Gonzalo a Zapopan.

${\color{Green} {2v}}+6({\color{Green} {v}}-{\color{Green} {30}})={\color{Green} {604}}$

Ahora, completa los espacios correspondientes. Al finalizar da clic en Verificar para recibir retroalimentación.

Propiedad distributiva:	$2v$ + $6v$ - $180$ = $604$
Sumas $180$	$2v+6v-$ $180$ + $180$ $=604+$ $180$
Simplificas:	$8v$ = $784$
Divides entre $8$	$\frac{8v}{8} = \frac{784}{8}$
Solución de la ecuación:	$v=$ $v=98$

Solución. La velocidad que lleva Gonzalo durante las dos primeras horas del viaje es de

$98$

km/h.

Verifica la solución sustituyendo el valor en la ecuación que plantea el problema.

$2v+6(v-30)=604$

$2(\color{green}{98})+6(\color{Green}{98}-30)=604$

${\color{Green} {196}}+6({\color{Green} {68}})=604$

${\color{Green} {196}}+{\color{Green} {408}}=604$

$604=604$

arriba

Problemas de velocidad

Formulario de búsqueda