Conversiones a fracciones a partir de números con series decimales infinitas
Otra de las formas de notación decimal que se tiene es la de sucesiones de dígitos infinitas, para comprobar que éstas también forman parte de los números racionales, haz clic en cada número para ver el procedimiento.
Revisa el proceso dando clic en los números
x=0.333333333333333…
Nombremos “x” al número decimal original que está representado como una serie infinita de dígitos que se repiten. Puede identificarse que el patrón de repetición es el “3”. La longitud del patrón de repetición es de una cifra.
x=0.333333333333333…
Nombremos “x” al número decimal original que está representado como una serie infinita de dígitos que se repiten. Puede identificarse que el patrón de repetición es el “3”. La longitud del patrón de repetición es de una cifra.
10x=3.333333333333333…
Multiplica por 10 ambos lados de la ecuación.
x=0.333333333333333…
Nombremos “x” al número decimal original que está representado como una serie infinita de dígitos que se repiten. Puede identificarse que el patrón de repetición es el “3”. La longitud del patrón de repetición es de una cifra.
10x=3.333333333333333…
Multiplica por 10 ambos lados de la ecuación.
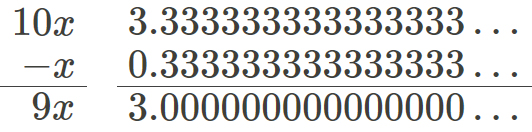
Realiza la resta 10x–x
x=0.333333333333333…
Nombremos “x” al número decimal original que está representado como una serie infinita de dígitos que se repiten. Puede identificarse que el patrón de repetición es el “3”. La longitud del patrón de repetición es de una cifra.
10x=3.333333333333333…
Multiplica por 10 ambos lados de la ecuación.
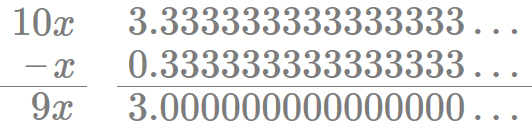
Realiza la resta 10x–x
9x=3
Finalmente tenemos esta expresión.
x=0.333333333333333…
Nombremos “x” al número decimal original que está representado como una serie infinita de dígitos que se repiten. Puede identificarse que el patrón de repetición es el “3”. La longitud del patrón de repetición es de una cifra.
10x=3.333333333333333…
Multiplica por 10 ambos lados de la ecuación.
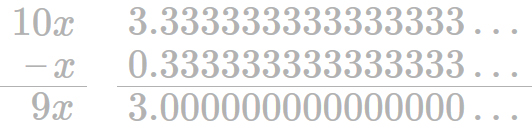
Realiza la resta 10x–x
9x=3
Finalmente tenemos esta expresión.
x=39
Despejando x, obtenemos una fracción equivalente.
El proceso es muy similar al visto para obtener una fracción, y consiste en eliminar, mediante una ecuación, los decimales que se repiten como una serie infinita.
Resumen del procedimiento
- 1. Identifica al número en su representación decimal.
- 2. Identifica cuántas cifras después del punto tiene el número en su representación decimal. Nombra n a este conteo.
- 3. Multiplica el numerador y el denominador por 10, el número de veces indicado en el conteo anterior (n); es decir, si hay dos decimales, tendrás que multiplicar dos veces por 10×10=100.
- 4. Si así lo deseas, puedes simplificar para obtener una fracción equivalente con numerador y denominador más simples.
Practicando
A continuación ejercitarás el procedimiento para obtener la representación en fracción de una cantidad decimal con una serie infinita de dígitos como x = 0.666666666666666… Para ello:
- Haz clic en cada número.
- Completa lo que se te pide en cada paso del procedimiento escribiendo en el espacio correspondiente.
- Al finalizar haz clic en Verificar para recibir retroalimentación.


