Fracciones con mismo signo pero numerador y denominador diferentes
Si dos o más fracciones tienen numerador y denominador diferentes, pero mismo signo, entonces es posible determinar el orden entre ellas mediante la multiplicación de las fracciones por un número múltiplo de sus denominadores; para ello es conveniente utilizar el mínimo común múltiplo (m.c.m). Este proceso simplifica la ordenación de los números racionales pues se reduce el análisis a la simple comparación de números enteros.
Por ejemplo, para determinar el orden entre los números positivos 45 y 67 se determina el mínimo común múltiplo de sus denominadores, cuyo valor es 35, que es resultado de la multiplicación de 7x5.

Entonces se multiplican ambas fracciones por el m.c.m.:
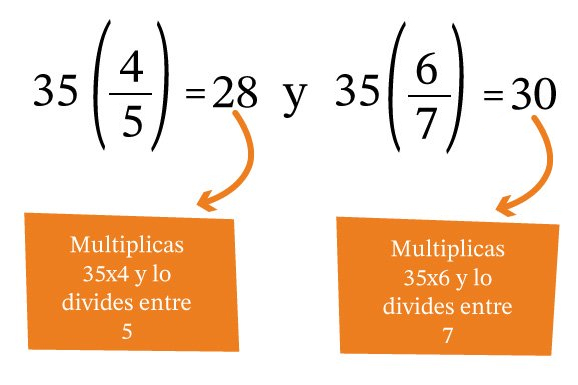
Como el primer número (28) es menor al segundo (30), entonces la primera fracción es menor que la segunda, es decir:
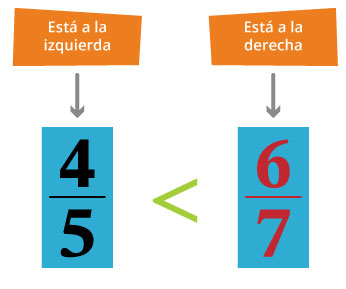
45<67
Este resultado se ilustra en la figura siguiente; se observa que 45 está a la izquierda de 67.
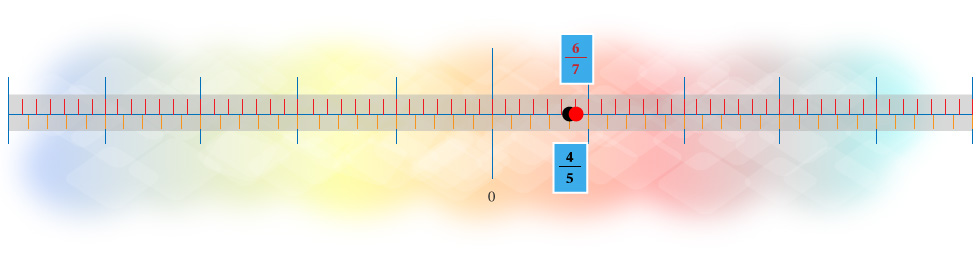
Ejemplo
Determinar el orden de los números −611 y −295
Para determinar el orden entre los números indicados, se calcula el m.c.m. de los denominadores, cuyo valor es 55, que es resultado de la multiplicación 11x5.
Ambas fracciones se multiplican por el m.c.m., lo que resulta en
−(55)611=−30 y −(55)295=−319
Como el primer resultado (−30) es mayor al segundo (−319), entonces la primera fracción es mayor que la segunda, es decir:
−611>−295
Este resultado se ilustra en la figura siguiente; se observa que −611 está a ala derecha de −295.
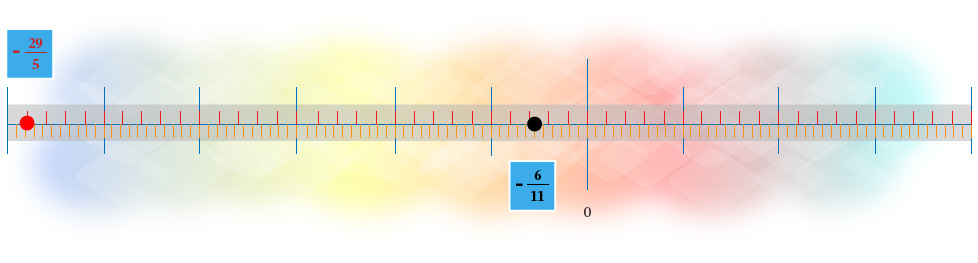
Ejemplo
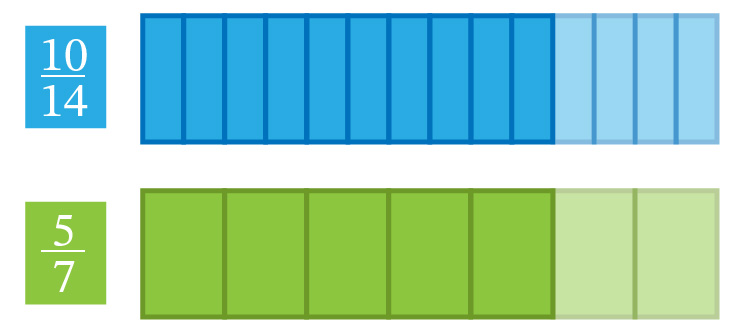
Determinar el orden de los números 57 y 1014
Para determinar el orden entre los números indicados, se calcula el m.c.m. de los denominadores, cuyo valor es 14.
Ambas fracciones se multiplican por el m.c.m., lo que resulta en:
(14)57=10 y (14)1014=10
Como los dos números son iguales, entonces se dice que las fracciones son equivalentes ya que representan la misma cantidad. Es decir:
57=1014
Este resultado se ilustra en la figura siguiente; se observa que ambas fracciones representan la misma cantidad.
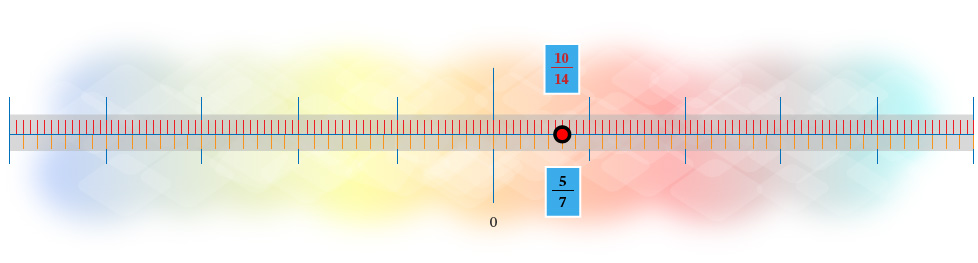
En la siguiente figura se muestra que la posición de las fracciones coincide en la recta numérica.
Este método es bastante práctico y puedes utilizarlo para determinar el orden y la equivalencia entre cualesquiera dos o más fracciones.

Utiliza el siguiente recurso GeoGebra para comparar números racionales con el mismo numerador.
- Selecciona el botón Fracciones con mismo numerador y denominador diferentes para que el objeto genere dos fracciones aleatorias que podrás comparar.
- Elige el símbolo adecuado de acuerdo al orden correspondiente (>, < o =).
- Da clic en Evaluar para revisar tu respuesta. En color verde se indicará el símbolo de orden correspondiente; mientras que en la recta numérica se mostrarán las posiciones que tienen.
- Para generar otro par de números racionales haz clic sobre el botón Reiniciar.
En la siguiente pantalla se profundizará en el manejo de las fracciones equivalentes.


