Sistemas triangulares: Procedimiento
Para obtener un sistema equivalente en forma triangular se deben seguir estos pasos:
| Ecuación 1: | $2x+3y=16$ ...Ec.1 |
| Ecuación 2: | $4x-y=-3$ ...Ec.2 |
| Genera un sistema equivalente en donde multipliques la ecuación Ec.1 por -2 (esto se realiza para hacer que se elimine la incógnita de las $x$) y al hacer la suma con la ecuación 2 obtienes la ecuación Ec.3: | $\matrix{ {\;\;\underline {\matrix{ {{-4x-6y=-32}} \hfill \cr {{4x-y=-3}} \hfill \cr } } } \hfill \cr {\;\;\;\;} \hfill \cr }$ $-7y =-35$ ...Ec.3 |
| El sistema de ecuaciones se transformó en un sistema escrito en forma triangular: |  |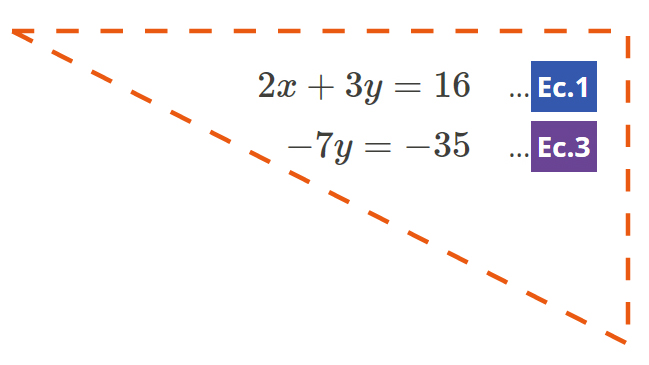
| Para encontrar la solución, despeja $y$ de la ecuación Ec.3 | $y=\frac{-35}{7}=5$ |
Sustituye $y= 5$ en la ecuación Ec.1: Despeja $x$: |
$2x+3y=16$ ...Ec.1 $2x+3 (5)=16$ $2x+15=16$ $x=\frac{16-15}{2}= \frac{1}{2}$ |
Comprobación
Para la comprobación, se sustituyen los valores de $x=\frac{1}{2}$ e $y=5$ en las ecuaciones Ec.1 y Ec.2, se debe cumplir la identidad en las dos.
| Sustituyendo en Ec.1 | Sustituyendo en Ec.2 |
|---|---|
$2(\frac{1}{2})+3(5)=16$ $16=16$ |
$4(\frac{1}{2})-(5)=-3$ $-3=-3$ |
Observa el resultado de las ecuaciones, en las que se cumple la igualdad en ambas con $x=\frac{1}{2}$, $y=5$, por lo que las soluciones encontradas son correctas.
Practicando
En el ejercicio anterior se pueden tener varios sistemas equivalentes para resolver el sistema original. Si el mismo sistema se multiplica por un número diferente se puede tener un sistema equivalente. A continuación multiplica por $-\frac{1}{2}$ la ecuación Ec.2 y escribe tu respuesta en los espacios correspondientes. Al terminar da clic en verificar para recibir retroalimentación.