Problema de número de diagonales de un polígono convexo
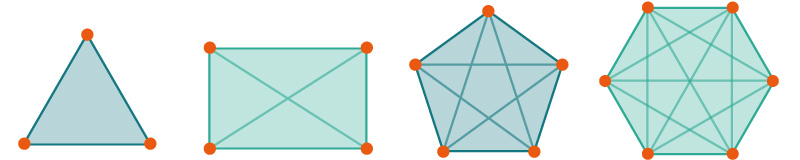
La diagonal de un polígono es un segmento de recta que une cualesquiera dos vértices no adyacentes o no consecutivos.
El número de diagonales está determinado por el número de lados que tiene el polígono.
Por ejemplo, en el caso del cuadrado:
- Tiene cuatro lados, por lo que n = 4
- De cada vértice parte sólo una diagonal, por lo que d = 1
- En total el cuadrado tiene D = 2 diagonales
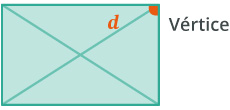
n representa el número de lados del polígono.
d representa el número de diagonales que parten de UN solo vértice.
D representa el número de diagonales en un polígono dado.
Con base en las diagonales de los polígonos regulares realiza lo siguiente:
- Completa la tabla que se te presenta hasta un polígono de nueve lados, para ello cuenta el número de diagonales que salen de UN solo vértice del polígono (d ).
- Posteriormente, para encontrar el número de diagonales del polígono según el número de lados, (D) considera el total de diagonales que salen de un solo vértice.
- Una vez que termines de llenar la tabla hasta un polígono de nueve lados, busca un patrón que te permita determinar las diagonales de un polígono de 50 lados.
- Después de observar cómo se va comportando el número de diagonales, según el número de lados del polígono, expresa la regla general que te permita encontrar el número de diagonales de un polígono de n lados; para ello se te proporciona una ayuda que deberás completar.
Al finalizar da clic en Verificar para recibir retroalimentación.
n - Representa el número de lados del polígono
d - Representa el número de diagonales que parten de UN solo vértice
D - Representa el número de diagonales en un polígono dado
Alumno: