Leyes de los exponentes

Como pudiste observar en el recurso GeoGebra, se obtuvieron potencias con igual base y el exponente indicado, lo que permite la formulación de la primera ley de los exponentes, la cual es:

$(a)^m\cdot{}(a)^n=(a)^{m+n}$

Ahora revisa los siguientes ejemplos y observa con atención la aplicación y desarrollo de la fórmula:

a (Base)	m (potencia)	n (potencia)	$a^m$	$a^n$	$a^m{\cdot{}a}^n$	$a^{m+n}$
2	4	5	$2^4$	$2^5$	$2^4{\cdot{}2}^5$	$2^9$
5	7	-9	$5^7$	$7^{-9}$	$5^7{\cdot{}5}^{-9}$	$5^{-2}$

Como pudiste observar en el recurso GeoGebra, al arrastrar los deslizadores se obtuvieron potencias con igual base y el exponente indicado en la división, lo cual permite la identificación de la regularidad que presenta la diferencia de sus exponentes para casos particulares y su generalización.

Ahora revisa los siguientes ejemplos en los que se muestran dos formas de obtener la división de dos potencias:

Primera forma: Restar los exponentes.

a (Base)	m (potencia)	n (potencia)	${(a)}^m$	${(a)}^n$	$\frac{{\left(a\right)}^m}{{\left(a\right)}^n}$	${\left(a\right)}^{m-n}$
2	9	5	${(2)}^9$	${(2)}^5$	$\frac{{\left(2\right)}^9}{{\left(2\right)}^5}=2^4$	$2^{9-5}=2^4$
7	8	-3	${(7)}^8$	${(7)}^{-3}$	$\frac{{\left(7\right)}^8}{{\left(7\right)}^{-3}}={\left(7\right)}^{11}$	$7^{8-(-3)}=7^{8+3}=7^{11}$
5	3	3	${(5)}^3$	${(5)}^3$	$\frac{{\left(5\right)}^3}{{\left(5\right)}^3}=1$	$5^{3-3}=5^0=1$

Cabe mencionar que, en la división de dos potencias con el mismo exponente, la potencia resultante tiene como exponente 0 y como toda potencia elevada al exponente 0 es 1, justifica que $\frac{5^1}{5^1}=5^{1-1}=5^0$, por lo que se concluye que $a^{0}=1$, y para el caso general $5^0=1$, para $a\not=0$.

Segunda forma: Representar las potencias como una multiplicación y simplificarlas.

---

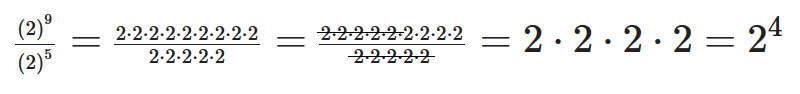
$\frac{{\left(7\right)}^8}{{\left(7\right)}^{-3}}={\left(7\right)}^8{{\left(7\right)}^3={\left(7\right)}^{8+3}=\left(7\right)}^{11}$, recordemos que $\frac{1}{7^{-3}}=7^3$ y que el producto de potencias como base igual, se suman los exponentes.

---

$\frac{{\left(5\right)}^3}{{\left(5\right)}^3}=\frac{5\cdot{}5\cdot{}5}{5\cdot{}5\cdot{}5}=1$

Con el recurso anterior puedes observar que al arrastrar los deslizadores se obtiene una potencia y luego la potencia de la potencia, lo que permite la identificación de la regularidad que presenta el producto de los exponentes para casos particulares y su generalización, y con ello la formulación de la tercera ley de los exponentes:

${\left(a^m\right)}^n={\left(a\right)}^{mn}$

Ahora observa los siguientes ejemplos en los que se muestran dos formas de obtener la división de dos potencias:

Primera forma: Multiplicar los exponentes de la primera y segunda potencia.

a (Base)	m (potencia)	n (potencia)	${(a)}^m$	$(a^m)^n$	$a^{mn}$
$\frac{3}{2}$	5	3	${\left(\frac{3}{2}\right)}^{3}$	${\left({\left(\frac{3}{2}\right)}^5\right)}^3$	${\left(\frac{3}{2}\right)}^{15}$
-7	2	5	${(-7)}^2$	${\left({\left(-7\right)}^2\right)}^5$	${(-7)}^{10}$

Segunda forma: Representar la multiplicación repetida de la primera potencia como lo indica el exponente de la segunda potencia, y como son potencias de la misma base se suman los exponentes.

${\left({\left(\frac{3}{2}\right)}^5\right)}^3={\left(\frac{3}{2}\right)}^5\cdot{}{\left(\frac{3}{2}\right)}^5\cdot{}{\left(\frac{3}{2}\right)}^5={\left(\frac{3}{2}\right)}^{15}$

---

${\left({\left(-7\right)}^2\right)}^5={\left(-7\right)}^2\cdot{}{\left(-7\right)}^2\cdot{}{\left(-7\right)}^2\cdot{}{\left(-7\right)}^2\cdot{}{\left(-7\right)}^2={\left(-7\right)}^{10}$

---

La generalización de los ejemplos particulares es mediante la expresión ${\left(a^m\right)}^n=a^m\cdot{}\ a^m\cdot{}a^m\cdot{}a^m\cdot{}a^m\cdot{},…,a^m\cdot{}a^m$, n veces el producto $a^m$. El producto de n veces la potencia $a^m$, significa la suma de $n$ veces $m$, la cual se escribe como $mn$, luego ${\left(a^m\right)}^n=a^{mn}$.

A través del recurso anterior pudiste observar que al arrastrar los deslizadores se obtuvieron potencias con base diferente e igual exponente, lo que te permitió la formulación de la quinta ley de los exponentes:

${\left(ab\right)}^m=a^mb^m$

Ahora revisa el siguiente ejemplo en el que se aplica esta ley:

a (Base)	m (potencia)	n (potencia)	${(ab)}^m$	Producto de $m$ veces $(ab)$	${\left(a\right)}^m\cdot{}{\left(b\right)}^m$
-7	2	5	${\left(-7\cdot{}2\right)}^5$	$\left(-7\cdot{}2\right)\cdot{}\left(-7\cdot{}2\right)\cdot{}\left(-7\cdot{}2\right)\cdot{}$ $\left(-7\cdot{}2\right).\left(-7\cdot{}2\right)={\left(-7\right)}^5\cdot{}2^5$	${\left(-7\right)}^5\cdot{}{\left(2\right)}^5$

El ejemplo muestra que se cumple la ley ${\left(ab\right)}^m=a^mb^m$ para casos particulares. Ahora pasamos a la comprobación de la ley considerando las bases $a$ y $b$ de cualquier número real y con exponente $m$. Al desarrollar la potencia se tiene ${\left(ab\right)}^m=\left(ab\right)\cdot{}\left(ab\right)\cdot{}\left(ab\right)\cdot{}\left(ab\right)\cdot{}\left(ab\right),…,\ \left(ab\right)\cdot{}\left(ab\right)$, $m$ veces el producto $(ab)$ , es decir, ${\left(ab\right)}^m=(a\cdot{}a\cdot{}a\cdot{}a\cdot{}a,…,\ a\cdot{}a)(b\cdot{}b\cdot{}b\cdot{}b\cdot{}b.,…,b\cdot{}b$, por lo que ${\left(ab\right)}^m={\left(a\right)}^m\cdot{}{\left(b\right)}^m$.

Con el recurso anterior pudiste observar que al arrastrar los deslizadores se obtuvieron potencias con base diferente e igual exponente, lo que permite la formulación de la quinta ley de los exponentes:

${\left(\frac{a}{b}\right)}^m=\frac{a^m}{b^m}$

Ahora revisa la siguiente tabla en la que se presentan dos ejemplos con los que se aplica esta ley.

a (Base)	m (potencia)	n (potencia)	${\left(\frac{a}{b}\right)}^m$	$\frac{{\left(a\right)}^m}{{\left(b\right)}^m}$
2	3	5	${\left(\frac{2}{3}\right)}^5$	$\frac{{\left(2\right)}^5}{{\left(3\right)}^5}$
3	-7	6	${\left(\frac{3}{-7}\right)}^6$	$\frac{{\left(3\right)}^6}{{\left(-7\right)}^6}$

Comprobación de que se cumple la ley para los valores especificados en la tabla:

$\left ( \frac{2}{3} \right )^{5}=\left ( \frac{2}{3} \right )\cdot \left ( \frac{2}{3} \right )\cdot \left ( \frac{2}{3} \right )\cdot \left ( \frac{2}{3} \right )\cdot \left ( \frac{2}{3} \right )=\frac{2^{5}}{3^{5}}$ por lo que $\left ( \frac{2}{3} \right )^{5}=\frac{2^{5}}{3^{5}}$

$\left ( \frac{3}{-7} \right )^{6}=\left ( \frac{3}{-7} \right )\cdot \left ( \frac{3}{-7} \right )\cdot \left ( \frac{3}{-7} \right )\cdot \left ( \frac{3}{-7} \right )\cdot \left ( \frac{3}{-7} \right )\cdot \left ( \frac{3}{-7} \right )=\frac{3^{6}}{-7^{6}}$ por lo que $\left ( \frac{3}{-7} \right )^{6}=\frac{3^{6}}{-7^{6}}$

Los ejemplos muestran que se cumple la ley $\left ( \frac{a}{b} \right )^{m}=\frac{(a)^{m}}{(b)^{m}}$ para casos particulares. Ahora se pasa a la generalización de la ley considerando las bases $a$ y $b$ cualesquiera números reales y exponente $m$. Al desarrollar la potencia del cociente se tiene $\left ( \frac{a}{b} \right )^{m}=\left ( \frac{a}{b} \right )\cdot \left ( \frac{a}{b} \right )\cdot \left ( \frac{a}{b} \right )\cdot \left ( \frac{a}{b} \right )\cdot \left ( \frac{a}{b} \right )\cdot ,...,\cdot \left ( \frac{a}{b} \right )\cdot \left ( \frac{a}{b} \right )$, $m$ veces el producto $\left(\frac{a}{b}\right)$, es decir, ${\left(\frac{a}{b}\right)}^m=\frac{\left(a\cdot{}a\cdot{}a\cdot{}a\cdot{}a.,…,a\cdot{}a\right)}{b\cdot{}b\cdot{}b\cdot{}b\cdot{}b.,…,b\cdot{}b}=\frac{{\left(a\right)}^m}{b^m}$, por lo que $\left ( \frac{a}{b} \right )^{m}=\frac{(a)^{m}}{(b)^{m}}$.