¿Cómo sumar dos fracciones que tienen diferente denominador, por ejemplo $\frac{1}{2}+\frac{1}{3}$?

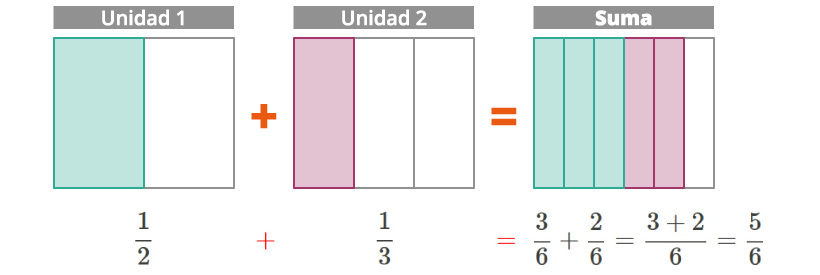
Como las fracciones son partes de una unidad pero de diferente tamaño, para poder sumarlas tenemos que convertirlas en partes del mismo tamaño, es decir, fracciones equivalentes que tengan el mismo denominador (denominador común). Una forma de lograr esto es multiplicando el numerador y el denominador de una de las fracciones por el denominador de la otra fracción:

En la primera fracción multiplicamos 1 y 2 (numerador y denominador, respectivamente) por 3 (denominador de la segunda fracción); mientras que, para la segunda fracción, multiplicamos 1 y 3 (numerador y denominador, respectivamente) por 2 (denominador de la primera fracción).

Las fracciones equivalentes que se obtienen son: $\frac{3}{6} + \frac{2}{6}$

Ya teniendo las fracciones con partes del mismo tamaño: $\frac{1}{6}\ $ (el denominador común es 6), podemos proceder a sumar los numeradores dejando el mismo denominador, como se muestra a continuación.

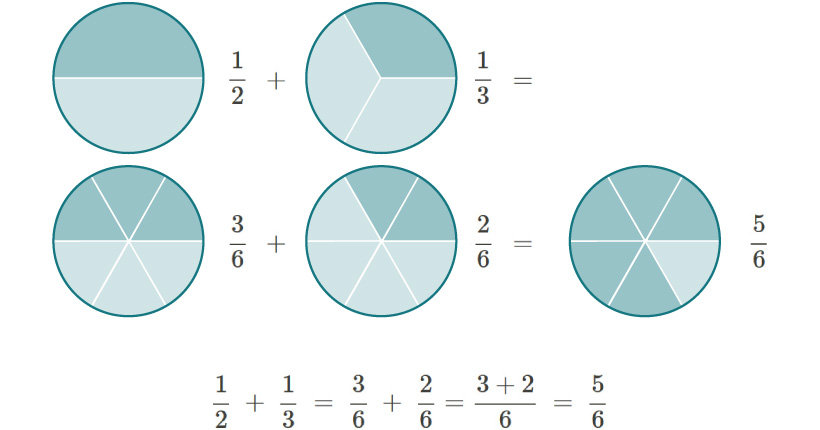
Este ejemplo lo podemos visualizar en los siguientes diagramas circulares :

La suma $\frac{4}{5}+\frac{3}{2}=\frac{4(2)}{5(2)}+\frac{3(5)}{2(5)}=\frac{8}{10}+\frac{15}{10}=\frac{8+15}{10}=\frac{23}{10}=2\frac{3}{10}$, porque el 10 cabe 2 veces en el 23 y sobran $\frac{3}{10}$.

(fracción mixta: 2 unidades más $\frac{3}{10}$)

También podemos efectuar la suma de la siguiente manera:

Como puedes observar, de igual forma que en el procedimiento anterior, cada numerador de las fracciones se multiplica por el denominador de la fracción contraria. Es decir, 4 (numerador de la primera fracción) por 2 (denominador de la segunda fracción), y el 3 (numerador de la primera fracción) por el 5 (denominador de la segunda fracción). Sin embargo, a diferencia del ejemplo previo, solamente se multiplica una vez el 5 denominador de la primera fracción) por el 2 (denominador de la segunda fracción), pues de ambas formas se obtiene el mismo resultado (10).

¿Cómo restar dos fracciones que tienen diferente denominador, por ejemplo $\frac{3}{4}-\frac{2}{5}$?

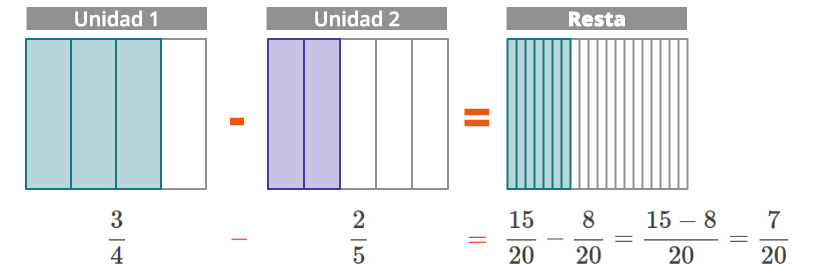
Procedemos de manera similar como en la suma. Para poder restar ambas fracciones tenemos que convertirlas en partes del mismo tamaño, es decir, fracciones equivalentes que tengan el mismo denominador (denominador común), para después restar los numeradores y dejar el mismo denominador.

Entonces, en la primera fracción multiplicamos 3 y 4 (numerador y denominador, respectivamente) por 5 (denominador de la segunda fracción); mientras que, para la segunda fracción, multiplicamos 2 y 5 (numerador y denominador, respectivamente) por 4 (denominador de la primera fracción).

Las fracciones equivalentes que se obtienen son: $\frac{15}{20} - \frac{8}{20}$

Ya teniendo las fracciones con partes del mismo tamaño $\frac{1}{20}$ (el denominador común es 20), podemos proceder a restar los numeradores, como se muestra a continuación.

También podemos efectuar la resta de la siguiente forma:

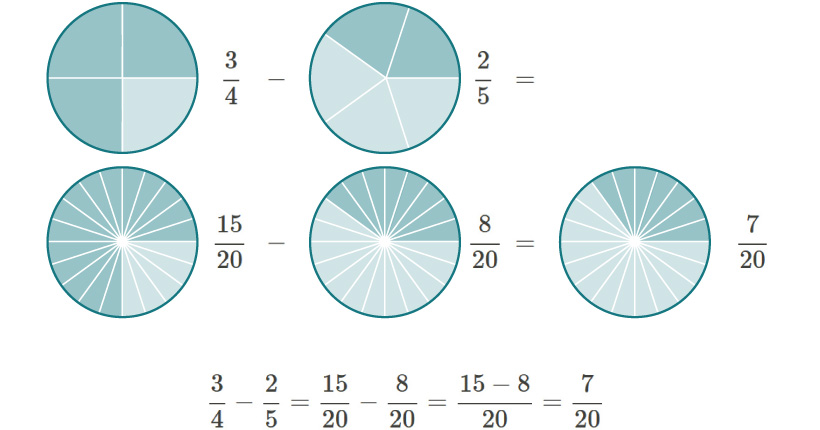
Este ejemplo lo podemos visualizar en los siguientes diagramas circulares:

¿Cuál es el resultado de la sustracción de dos fracciones con distinto denominador, si el minuendo es menor que el sustraendo? Veamos un ejemplo tomando las fracciones anteriores, pero restándolas en diferente orden: $\frac{2}{5}-\frac{3}{4}\ \ $

Se sigue el procedimiento anterior, pero el resultado que se obtiene es negativo:

También podemos efectuar la resta de forma similar a la suma, tomando en cuenta las reglas de los signos:

De los ejemplos anteriores se puede inferir que: