Paso 1. Recabar los datos conocidos

Distancia de Cuernavaca a la Cd. de México 83.7 km

Distancia de la Cd. de México a Pachuca 110.5 km

Paso 2. Realizar el procedimiento

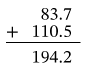
Respuesta

194.2 km

Paso 1. Recabar los datos conocidos

Pastel 1: $\frac{4}{15}$

Pastel 2: $\frac{1}{3}$

Paso 2. Realizar el procedimiento

$$\frac{4}{15}+\ \frac{1}{3}=\ \frac{\left(4)(1\right)+\left(5)(1\right)}{15}=\frac{4+5}{15}=\frac{9}{15}=\frac{3}{5}$$

Consulta el material de Adición y Sustracción de fracciones con diferente denominador para conocer cómo se hace el procedimiento de este tipo de operaciones.

Respuesta

Se repartieron $\frac{3}{5}$ de los pasteles

Paso 1. Recabar los datos conocidos

Total, que deja el hombre 9,500.00

Mayor recibe 2,300.00

Segundo recibe 2,300.00 - 500.00= 1,800.00

Tercero 2,300.00 + 1,800.00= 4,100.00

Paso 2. Realizar el procedimiento

9500 - 2300 – 1800- 4100 = 1300

Respuesta

La esposa recibe la cantidad de 1,300.00

Paso 1. Recabar los datos conocidos

Total pedido de carne 3000 kg

Primera entrega 854 kg

Segunda entrega 854 kg – 123 kg = 731 kg

Tercera entrega 854 kg + 156 kg = 1010 kg

Paso 2. Realizar el procedimiento

3000 - 854 – 731- 1010 = 405

Respuesta

Le faltan por enviar 405 kg de carne

Paso 1. Recabar los datos conocidos

Fracción $\ \frac{5}{9}$

Unidad en novenos $\ \frac{9}{9}$

Paso 2. Realizar el procedimiento

$$\frac{9}{9}-\ \frac{5}{9}=\ \frac{\left(9)(9\right)-\left(9)(5\right)}{81}=\frac{36}{81}=\frac{4}{9}$$

Respuesta

Le faltan $\ \frac{4}{9}$ para ser la unidad

Paso 1. Recabar los datos conocidos

1 día laborado a 780.00

12 días laborados

Paso 2. Realizar el procedimiento

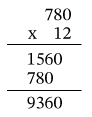
Respuesta

El trabajador recibirá por 12 días laborados 9,360.00

Paso 1. Recabar los datos conocidos

Practicó piano 5 días esta semana

Practicó $\frac{3}{4}$ de hora cada día

Paso 2. Realizar el procedimiento

$$(5)(\ \frac{3}{4})\ =\ \frac{(5\ )(3)}{4}\ =\ \frac{15}{4}=\ 3.75\ $$

Respuesta

Víctor practicó piano esta semana 3 horas más $\frac{3}{4}$ de hora

Paso 1. Recabar los datos conocidos

$\frac{1}{4}$ de un paquete de 750 g de azúcar.

$\frac{1}{3}$ de un paquete de harina de un kilogramo.

$\frac{1}{2}$ de una barra de mantequilla de 500 g.

Paso 2. Realizar el procedimiento

$(\ \frac{1}{4}\ )$ (750) = 187.5 gramos

$(\ \frac{1}{3}\ )\ $ (1000) = 333.33 gramos

$(\ \frac{1}{2}\ )$ (500) = 250 gramos

Respuesta

Se necesitan 187.5 gramos de azúcar, 333.33 gramos de harina y 250 gramos de mantequilla

Paso 1. Recabar los datos conocidos

Cosecha de 5,652 kg de naranja

Bolsas de 4.5 kg

Paso 2. Realizar el procedimiento

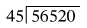
Se quita el punto del divisor y se aumenta un cero en el dividendo

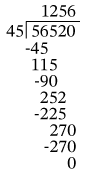
Respuesta

Se pueden llevar 1256 bolsas

Paso 1. Recabar los datos conocidos

La receta necesita $\frac{3}{4}$ de taza de arándanos

Si preparamos media receta

Paso 2. Realizar el procedimiento

$$\frac{3}{4}\ \div{}\ \ 2=\ \ \frac{3}{4}\ \div{}\ \ \frac{2}{1}=\ \frac{(3)(1)}{(4)\ (2\ )}=\ \frac{3}{8}$$

Respuesta

Necesitamos $\frac{3}{8}$ de taza de arándanos

Paso 1. Recabar los datos conocidos

Jarra de litro y medio de agua de limón

vasos de $\frac{1}{8}$ de litro cada uno

Paso 2. Realizar el procedimiento

$\frac{3}{2}\ \div{}\ \frac{1}{8}\ =\ \frac{(3)(8)}{(2)\ (1)}=\ \frac{24}{2}=12$

Respuesta

Se pueden repartir 12 vasos de agua de limón

Paso 1. Recabar los datos conocidos

$$8^{5}= 32768$$

Paso 2. Realizar el procedimiento

$$\ \ 8^5=\left(8\right)\ \left(8\right)\ \left(8\right)\ \left(8\right)\ \left(8\right)=\ 32768$$

Respuesta

$$8^{5}= 32768$$

Paso 1. Recabar los datos conocidos

Tres discos

Cifras del 1 al 3

Paso 2. Realizar el procedimiento

$$\ \ 3^3=\left(3\right)\ \left(3\right)\ \left(3\right)=\ 27$$

Respuesta

Las combinaciones son 27

Paso 1. Recabar los datos conocidos

Paso 2. Realizar el procedimiento

Para n horas se tienen 3n+ 1 bacterias

$$\ \ 3^{6+1}=\left(3\right)\ \left(3\right)\ \left(3\right)\ \left(3\right)\ \left(3\right)\left(3\right)\left(3\right)=\ 2187$$

Respuesta

Las bacterias que se existen a la sexta hora son 2,187

Paso 1. Recabar los datos conocidos

El doble del cuadrado de un número se le restan 9 el resultado es cero, es:

$$2x^2-9=0$$

Paso 2. Realizar el procedimiento

$$2x^2-9=0$$

Sumando 9 a ambos términos de la ecuación

$$2x^2-9+9=0+9$$

Nos resulta

$$2x^2=9$$

Dividiendo entre dos ambos términos de la ecuación

$$x^2=\ \frac{9}{2}$$

Aplicando la operación radicación en ambos términos de la ecuación

$$\sqrt{x^2}=\ \sqrt{\frac{9}{2}}$$

Nos resulta

$$x=\sqrt{\frac{9}{2}}$$

Lo que resulta

$$x=\ \frac{\sqrt{9}}{\sqrt{2}}$$

Aplicando las raíces

$$x=\ \frac{3}{\sqrt{2}}$$

Respuesta

El número buscado es $\ \frac{3}{\sqrt{2}}$

Comprobando:

Sustituyendo $x= \ \frac{3}{\sqrt{2}}$ en

$$2x^2-9=0$$

Resulta

$$2{(\frac{3}{\sqrt{2}})}^2-9=0$$

Aplicando el cuadrado al paréntesis

$$2(\frac{9}{2})-9=0$$

Y su resultado

$$9-9=0$$

Ya que se cumple la igualdad

Paso 1. Recabar los datos conocidos

Paso 2. Realizar el procedimiento

El área de un cuadrado es

$$\acute{a}rea=(lado)(lado)$$

$$\acute{a}rea=\ \left(l\right)\left(l\right)=l^2$$

$$1024\ alumnos=l^2$$

$$l=\ \sqrt{1024}$$

$$l=\ 32$$

Respuesta

32 alumnos van a estar en cada lado del cuadrado

Paso 1. Recabar los datos conocidos

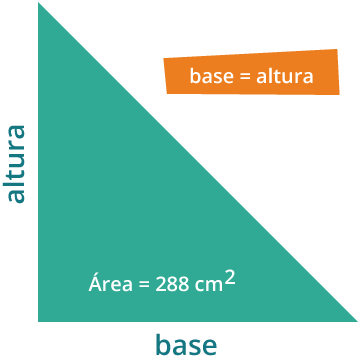
Paso 2. Realizar el procedimiento

El área de un triángulo es

$$\acute{a}rea=\frac{(base)(altura)}{2}$$

Como la base es igual a la altura

$$\acute{a}rea=\ \frac{(lado)(lado)}{2}$$

Sustituyendo el valor del área

$$288\ =\ \frac{{(lado)}^2}{2}$$

Despejando el lado, nos quedaría:

$$lado\ = \sqrt{(2)(288)}$$

$$lado = 24$$

Respuesta

La longitud de cada lado es de 24 cm