Sistema compatible con infinidad de soluciones
Ahora se resolverá un sistema compatible con infinidad de soluciones por el Método de Suma o Resta, teniendo como ejemplo las siguientes ecuaciones:
3x+4y=2 Ec. 1
6x+8y=4 Ec. 2
Igual que en los sistemas anteriores, esta solución está dada por la solución común de las dos ecuaciones, es decir, las coordenadas del punto de intersección de las gráficas de cada una de las ecuaciones como se revisará más adelante.
Practicando
Para determinar la solución del sistema por el Método de Suma o Resta deberás seguir el esquema de cuatro pasos que se ha venido trabjando, da clic en cada pestaña para revisarlos y completa los espacios correspondientes. Al finalizar da clic en Verificar para revisar tus respuestas.
Multiplicación de cada ecuación
Se multiplica cada ecuación por números que igualen los coeficientes de una misma incógnita en las dos ecuaciones para eliminar una de las incógnitas.
Se deben obtener ecuaciones equivalentes a las originales que, al sumarlas o restarlas, permitan eliminar la incógnita seleccionada para conseguir una ecuación con una sola incógnita.
Una vez más, para igualar los coeficientes de y como se hizo en el sistema anterior, se deberá multiplicar la Ec. 1 por el coeficiente 8 de y de la Ec.2 y multiplicar la Ec.2 por el coeficiente 4 de y de la Ec.1 como se hace a continuación:

Sumar o restar las ecuaciones
Se suman o se restan las ecuaciones Ec.1' y Ec.2' para eliminar una de las incógnitas. En este caso se restan algebraicamente para eliminar la incógnita y, con lo que se obtendría una ecuación con una sola incógnita x Ec.3 y se resuelve:
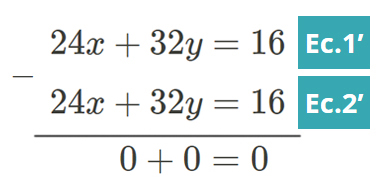
0=0 Ec.3
Pero ¿qué sucede? ¡Se eliminó también la otra incógnita x!
Esto es, se obtuvo la Ec.3 que no tiene incógnitas, pero se cumple la igualdad 0=0. Esto significa que para cualquier valor que tenga la incógnita x en la ecuación 1 o en la ecuación 2, se cumplirá siempre la ecuación Ec.3, por lo que el sistema tiene infinidad de soluciones como se verá a continuación.
Sustituir valores
Se sustituye el valor encontrado, en este caso el de x que se quiera, en cualquiera de las ecuacionesen que tiene a las dos incógnitas para encontrar el valor de la otra incógnita. En este caso se escoge sustituir en la Ec. 1:
Por ejemplo:
Comprobación
Se sustituye la solución encontrada en cada una de las dos ecuaciones originales para verificar que se cumpla la igualdad.


