Sistema incompatible sin solución
A continuación se revisará un sistema incompatible sin solución, teniendo como ejemplo el siguiente sistema de ecuaciones lineales por el Método de Suma o Resta:
3x+2y=5 Ec. 1
6x+4y=3 Ec. 2
Como en los sistemas anteriores, la solución estará dada por el resultado común de las dos ecuaciones, es decir, las coordenadas del punto de intersección de las gráficas de cada una de las ecuaciones como se verá al final.
Para determinar la solución del sistema por el Método de Suma o Resta revisa los pasos dando clic en cada pestaña:
Multiplicación de cada ecuación
Se multiplica cada ecuación por números que igualen los coeficientes de una misma incógnita en las dos ecuaciones para eliminar una de las incógnitas. Al hacer esto se obtienen ecuaciones equivalentes a las originales que, al sumarlas o restarlas, conllevan la eliminación de esa incógnita y se obtiene una ecuación con la otra incógnita solamente.
Una forma de lograr esto, para igualar los coeficientes de y como se hizo en el sistema anterior, es multiplicar la Ec. 1 por el coeficiente 4 de y de la Ec.2 y multiplicar la Ec.2 por el coeficiente 2 de y de la Ec.1 como se hace a continuación:

De Ec.1 4(3x+2y=5) se obtiene 12x+8y=20 Ec.1’
De Ec.2 2(6x+4y=3) se obtiene 12x+8y=6 Ec.2’
Sumar o restar las ecuaciones
Se suman o se restan las ecuaciones Ec.1' y Ec.2' para eliminar una de las incógnitas. En este caso se restan algebraicamente para eliminar la incógnita y, con lo que se obtendría una ecuación con una sola incógnita x Ec.3 y se resuelve:
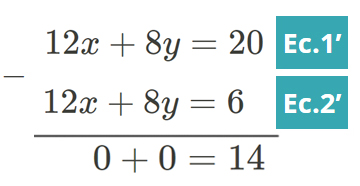
0=14 Ec.3
Pero qué sucede … ¡se eliminó también la otra incógnita x!
Esto es, se obtuvo la Ec.3 que no tiene incógnitas, pero NO se cumple la igualdad 0=14. Esto significa que para cualquier valor que tenga la incógnita x en la ecuación 1 o en la ecuación 2, NO se cumplirá la ecuación Ec.3, por lo que el sistema NO tiene solución como se verá también a continuación.
Si se multiplican los dos lados de la ecuación Ec.1 3x+2y=5 por 2, para conservar la igualdad, 2(3x+2y)=2(5), se obtiene la ecuación equivalente a Ec.1: 6x+4y=10; mientras que la condición de la ecuación original Ec.2 es 6x+4y=3, por lo que cualquier punto (x, y) que cumple con la Ec.1 NO cumple con la Ec.2, y viceversa, ya que 6x+4y NO tiene el mismo valor en las dos ecuaciones a la vez, pues en la primera su valor es 10 y en la segunda su valor es 3.
Por lo que se concluye que el sistema NO tiene solución
Este sistema de ecuaciones lineales es un Sistema incompatible, sin solución. Por lo tanto, ya no se pueden seguir los pasos 3 y 4.
Ahora revisa el siguiente recurso GeoGebra sobre el Sistema incompatible sin solución. en el que observarás las diferentes coordenadas de los puntos A y B que cumplen con cada una de las ecuaciones del sistema, así como los puntos de intersección de las gráficas que darían la solución al sistema de ecuaciones.



