División de fracciones
Revisa el siguiente acordeón, en éste se muestran ejemplos en los que se explica cómo se lleva a cabo la resolución de división de fracciones.
Ejemplo 1
La división de $\frac{1}{2}$ entre $2$ se puede interpretar como la mitad de $\frac{1}{2}$ como se ilustra en los diagramas circulares:
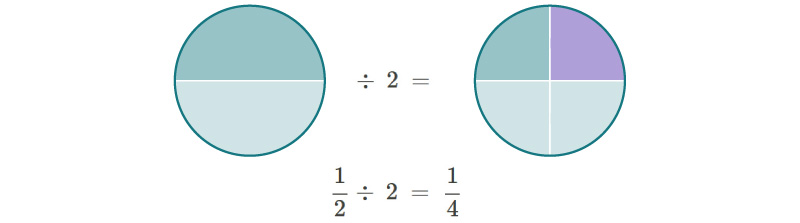
La unidad se divide en medios y se toma un medio (parte izquierda).
De $\frac{1}{2}$ se toma la mitad (parte derecha). La parte violeta es la mitad de $\frac{1}{2}$, que a su vez representa $\frac{1}{4}$. Por tanto, un medio entre dos = $\frac{1}{2}\div{}\ 2\ =\ \frac{1}{4}$
Ejemplo 2
Observa el siguiente ejemplo e interprétalo de manera similar al anterior:
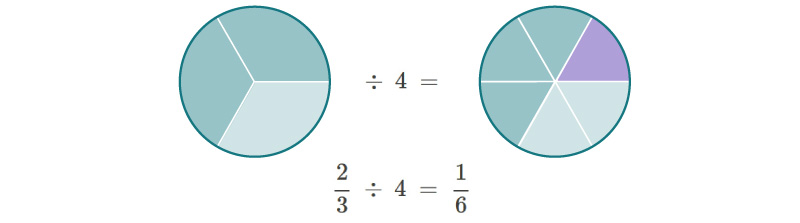
La parte violeta es la cuarta parte de $\frac{2}{3}$ que a su vez representa $\frac{1}{6}$.
La división de dos números racionales se puede ver a través de una multiplicación de manera similar que con los números enteros siguiendo las reglas de los signos, por ejemplo:
Con números enteros:
${\color{Blue} 6}\div{}\ {\color{Green} 3}\ =\ {\color{Red} 2}$ ya que ${\color{Green} 3}\cdot {\color{Red} 2}= {\color{Blue} 6}$
${\color{Blue} {20}}\div {\color{Green} 5}= {\color{Red} 4}$ ya que ${\color{Green} 5}\cdot {\color{Red} 4}= {\color{Blue} {20}}$
${\color{Blue} {-12}}\div {\color{Green} 4}= {\color{Red} {-3}}$ ya que ${\color{Green} 4}\cdot ({\color{Red} -}{\color{Red} 3})= {\color{Blue} -}{\color{Blue} {12}}$
Con números racionales:
$\frac{{\color{Blue} 2}}{{\color{Blue} 5}} \div{} \frac{{\color{Green} 1}}{{\color{Green} 3}}\ =\frac{{\color{Red} 6}}{{\color{Red} 5}}$ ya que $\frac{{\color{Green} 1}}{{\color{Green} 3}}\ \div{} \frac{{\color{Red} 6}}{{\color{Red} 5}}\ =\frac{6}{15}=\frac{{\color{Blue} 2}}{{\color{Blue} 5}}$
$\frac{{\color{Blue} 2}}{{\color{Blue} 3}}\div \frac{{\color{Green} 5}}{{\color{Green} 4}}=\frac{{\color{Red} 8}}{{\color{Red} {15}}}$ ya que $\frac{{\color{Green} 5}}{{\color{Green} 4}}\cdot \frac{{\color{Red} 8}}{{\color{Red} {15}}}=\frac{40}{60}=\frac{{\color{Blue} 2}}{{\color{Blue} 3}}$
${\color{Blue} -}\frac{{\color{Blue} 3}}{{\color{Blue} 4}}\div \frac{{\color{Green} 5}}{{\color{Green} 2}}={\color{Red} -}\frac{{\color{Red} 6}}{{\color{Red} {20}}}$ ya que $\frac{{\color{Green} 5}}{{\color{Green} 2}}\cdot \left ( {\color{Red} -}\frac{{\color{Red} 6}}{{\color{Red} {20}}} \right )=-\frac{30}{40}={\color{Blue} -}\frac{{\color{Blue} 3}}{{\color{Blue} 4}}$
El cociente $\frac{{\color{Red} 6}}{{\color{Red} 5}}$ se puede ver como el resultado de multiplicar en cruz el dividendo $\frac{{\color{Blue} 2}}{{\color{Blue} 5}}$ y el divisor $\frac{{\color{Green} 1}}{{\color{Green} 3}}$ , como se muestra en el siguiente diagrama. De manera similar la otra división.
De los ejemplos se puede inferir que:
La división de dos fracciones se puede obtener multiplicando en cruz como se muestra en el diagrama siguiente:
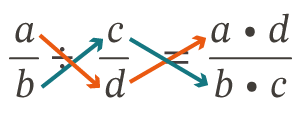
La multiplicación del numerador $a$ de la primera fracción por el denominador $d$ de la segunda fracción es el numerador del resultado $a\bullet{}d$.
La multiplicación del denominador $b$ de la primera fracción por el numerador $c$ de la segunda fracción es el denominador del resultado $b\bullet{}c$.
Revisa el recurso GeoGebra que se presenta. Observa que el resultado de dividir fracciones se encuentra con la fórmula que se presentó previamente.
