La raíz tiene los siguientes elementos
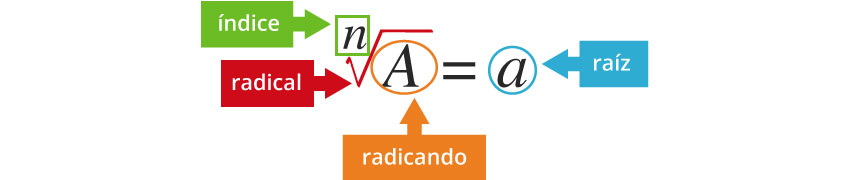
La radicación, aritméticamente es otra forma de expresar una potenciación, ya que el exponente es un número racional, es decir:
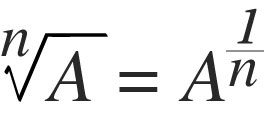
Por ejemplo:
$$\sqrt[2]{4}={4\ }^{\frac{1}{2}}= 2$$ $$\sqrt[3]{27}={27\ }^{\frac{1}{3}}= 3$$ $$\sqrt[4]{625}={625\ }^{\frac{1}{4}}=5$$
Si quieres saber más sobre cómo se realiza este proceso consulta el material Radicación.
Ahora revisa cómo se aplica la radicación para resolver algunos problemas
Una caja en forma cúbica tiene un volumen de $125,000 cm^3$, ¿Cuáles son las dimensiones de la caja?
Paso 1. Recabar los datos conocidos
Paso 2. Realizar el procedimiento
Para el cubo su volumen se define como
$$volumen=\ {arista}^3$$
Por lo que las dimensiones de sus aristas son
$$arista=\ \sqrt[3]{volumen}$$
$$arista=\ \sqrt[3]{125000}=50$$
Respuesta
El cubo va a tener 50 cm por cada arista.
¿Cuáles son las dimensiones de un terreno rectangular de 243 m2, si su longitud es el triple que su ancho?
Paso 1. Recabar los datos conocidos
Paso 2. Realizar el procedimiento
El área de un rectángulo es
$$\acute{a}rea=(largo)(ancho)$$
Y dice el enunciado que su longitud es el triple que su ancho
$$\acute{a}rea=\ 243=\left(3a\right)\left(a\right)=3a^2$$
$$243=3a^2$$
$$a^2=\frac{243}{3}=\ \ 81\ $$
$$a=\ \sqrt{81}$$
$a=\ 9$ y el largo $l=\ 3a$
$$l=\ 27$$
Respuesta
Las dimensiones del terreno son de ancho 9 metros y largo 27 metros.
Un terreno cuadrado tiene una superficie de 3,481 m2 y se quiere realizar una barda con malla que cuesta 4.50 cada metro. ¿Cuánto va a costar la barda?
Paso 1. Recabar los datos conocidos
Área del terreno 3,481 m2
La malla cuesta 4.50 cada metro
Paso 2. Realizar el procedimiento
El área de un cuadrado es
$$\acute{a}rea=(lado)(lado)$$
$$\acute{a}rea=\ \left(l\right)\left(l\right)=l^2$$
$$3481=l^2$$
$$l=\ \sqrt{3481}$$
$$l=\ 59$$
$$barda = (4) (lado) ($4.50) $$
$$barda = (4) (59) ($4.50) = 1062$$
Respuesta
La barda de 59 metros por lado y un total de 236 metros cuesta 1,062.00.