Análisis del parámetro a de la variación directa y=ax
En este apartado se retoman las actividades que desarrollaste y los aprendizajes que lograste sobre el concepto de variación directamente proporcional, para que analices el parámetro a de la expresión simbólica de la variación directa y=ax, y comprendas el efecto que le produce a la gráfica de la función.
Para ello, te apoyarás del recurso GeoGebra Análisis de la variación directa.
Con base en la interacción que realizaste con el recurso GeoGebra, lee las situaciones del parámetro a y escribe en la columna de la derecha la letra que corresponda, según el efecto que produce en cada caso.
Ahora revisa el siguiente ejemplo en el que se muestra el procedimiento para determinar la razón de cambio y la expresión simbólica de la variación directa, a partir de las coordenadas de los puntos P y Q que la satisfacen (los puntos están en la recta), tal como se muestra en la siguiente figura.
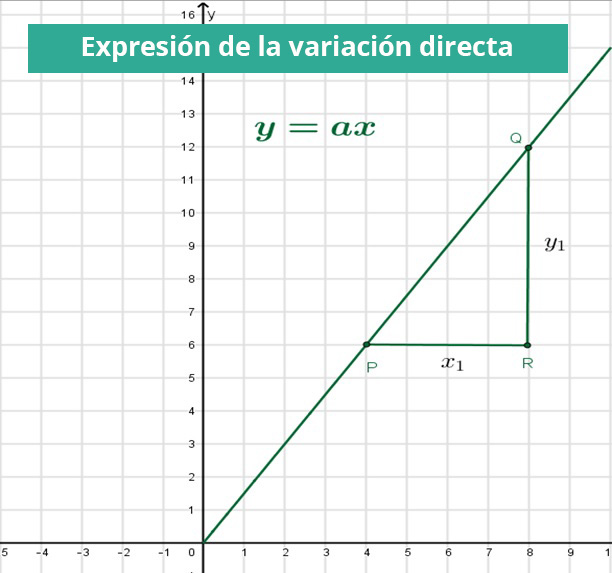
Recordemos que la variación directa es una función de x y tiene como expresión algebraica y=ax; para obtener su expresión simbólica en concordancia con la gráfica, debemos determinar el valor de su razón de cambio yx=a, para ello, consideramos que x1=4, y1=6, luego la razón de cambio es y1x1=64 y la expresión simbólica de la variación directa es y=64x.



