Problemas que involucran potenciación y radicación
En este apartado se presentan y resuelven algunos problemas que involucran a las potencias y los radicales para que comprendas sus aplicaciones en diversos campos del conocimiento Biología, Física, Ingeniería y Negocios, entre otros, así como la importancia de su estudio.
Da clic en cada pestaña para revisar los problemas
1) ¿Cuál es el capital que se obtiene al invertir $2,500 a un interés simple anual del 5%, durante cinco años?
Solución. Se determina el capital para cada año. Para el primero, éste se obtiene con la suma de la inversión y el interés, resultado de la multiplicación de la inversión por el interés. En la tabla se presenta la inversión para cada año y el capital mediante potencias.
| Años | Inversión | Capital |
|---|---|---|
| 1 | $2500$ | $2500+2500\left(0.05\right)=2500\left(1+0.05\right)$ |
| 2 | $2500\left(1+0.05\right)$ | $2500\left(1+0.05\right)+2500\left(1+0.05\right)\left(0.05\right)$ $=2500\left(1+0.05\right)\left(1+0.05\right)$ $=2500{\left(1+0.05\right)}^2$ |
| 3 | $2500{\left(1+0.05\right)}^2$ | $2500{\left(1+0.05\right)}^2+2500{\left(1+0.05\right)}^2\left(0.05\right)$ $=2500{\left(1+0.05\right)}^2\left(1+0.05\right)$ $=2500{\left(1+0.05\right)}^2=2500{\left(1+0.05\right)}^3$ |
| 4 | $2500{\left(1+0.05\right)}^3$ | $2500{\left(1+0.05\right)}^3+2500{\left(1+0.05\right)}^3\left(0.05\right)$ $=2500{\left(1+0.05\right)}^3\left(1+0.05\right)$ $=2500{\left(1+0.05\right)}^4$ |
| 5 | $2500{\left(1+0.05\right)}^4$ | $2500{\left(1+0.05\right)}^4+2500{\left(1+0.05\right)}^4\left(0.05\right)$ $=2500{\left(1+0.05\right)}^4\left(1+0.05\right)$ $=2500{\left(1+0.05\right)}^5$ |
El capital para el segundo año se obtiene con la suma de la inversión del segundo año y el interés correspondiente a ésta, y así sucesivamente para los años restantes, tal como se muestra en la tabla.
El capital conseguido al final de los cinco años con dos decimales es $2500(1+0.05)^{5}+2500(1.05)^{5}=2500(1.27)=$ 3,175. Cabe mencionar que al desarrollar la potenciación $(1.05)^5$ con la calculadora se consideró $1.27$.
2) La distancia de la Tierra al Sol es de $1.5\cdot 10^{8}$. Saturno se encuentra a una distancia 9.34 más alejado del Sol que la Tierra, ¿cuál es la distancia de Saturno al Sol?
Solución. Como Saturno se encuentra a una distancia de 9.34 más alejado del Sol que la Tierra, entonces su distancia es $9.34(1.5\cdot 10^{8})=9.34\cdot 1.5\cdot 10^{8}=14.01\cdot 10^{8}=1.401\cdot 10^{9}$.
Cabe mencionar que esta notación corresponde a la notación científica, en ésta se coloca el punto decimal después del primer dígito del número multiplicado por una potencia de diez que indica los lugares que se recorrerá el punto decimal a la derecha del mismo, cuando el exponente es positivo, y a la izquierda, cuando es negativo. En la solución del problema el punto decimal se recorrió a la izquierda y el exponente de la potencia se incrementó en uno.
3) El lenguaje de las computadoras es el sistema binario, se le denomina así ya que utiliza solamente los dígitos 0 y 1, a diferencia del sistema decimal que utiliza los dígitos desde el cero hasta el nueve, ambos sistemas son posicionales, ¿cuál es el equivalente decimal al binario 111011.101?
Solución. Recordemos que, para convertir números de cualquier base al sistema decimal, en particular, el número binario, éste se escribe como el desarrollo de sus potencias de dos (base) de acuerdo con la posición que ocupan sus dígitos a partir del punto decimal, a la izquierda de éste las posiciones de los dígitos se representan con los exponentes: 0, 1, 2, 3, 4 y 5, mientras que a la derecha con: -1, -2 y -3, tal como se ilustra a continuación:
$111011.101=1\cdot 2^{5}+1\cdot 2^{4}+1\cdot 2^{3}+0\cdot 2^{2}+1\cdot 2^{1}+1\cdot 2^{0}+1\cdot 2^{-1}+0\cdot 2^{-2}+1\cdot 2^{-3}=$
$1\cdot 32+1\cdot 16+1\cdot 8+0.4+1\cdot 2+1\cdot 1+\frac{1}{2}+\frac{0}{4}+\frac{1}{8}=$
$32+16+8+0+2+1+0.5+0+0.125=59.625$
Por lo que el número binario 111011.101 es equivalente al número decimal 59.625.
Para ampliar y reforzar el procedimiento para la conversión de números de cualquier base a la base decimal, se convierte el número en base octal 5723.51 a la base decimal. Recordemos que los ocho dígitos del sistema octal son 0, 1, 2, 3, 4, 5, 6, 7.
Solución. El procedimiento es similar a la conversión realizada para números binarios a la base decimal pero considerando potencias de ocho en lugar de potencias de dos, de acuerdo con la posición que ocupan sus dígitos a partir del punto decimal, a la izquierda de éste las posiciones de los dígitos se representan con los exponentes: 0, 1, 2 y 3, mientras que a la derecha con: -1 y -2, tal como se ilustra a continuación:
$5723.51=5\cdot{}8^3+7\cdot{}8^2+2\cdot{}8^1+3\cdot{}8^0+5\cdot{}8^{-1}+1.8^{-2}$
$=5\cdot 512+7\cdot 64+2\cdot 8+3\cdot 1+\frac{5}{8}+\frac{1}{64}$
$=2560+448+16+3+0.625+0.015625=3027.640625$
Por lo que el número octal, 5723.51 es equivalente al número decimal 3027.640625.
4) Determina la hipotenusa de la espiral de Teodoro para el triángulo rectángulo que tiene como catetos $1\ y\ \sqrt{7}$.
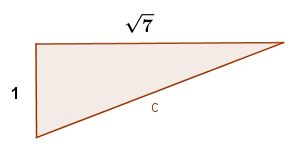
Solución. Aplicando el teorema de Pitágoras $c^{2}=a^{2}+b^{2}$, donde c es la hipotenusa, mientras que a y b son los catetos del triángulo rectángulo. Al sustituir los datos del problema en la expresión resulta $c^2=1^2+{\left(\sqrt{7}\right)}^2=1+7=8$. Por lo que la longitud de la hipotenusa del triángulo rectángulo es $c=\sqrt{8}$. Cabe mencionar que $1^{2}=1$ y $(\sqrt{7})^{2}=7$, puesto que la raíz cuadrada y la potencia se neutralizan. Por lo que $c^2=8$ y al extraer raíz cuadrada en ambos lados de la igualdad se obtiene $c=\sqrt{8}$.